圆锥曲线
TLE_Automat
·
·
个人记录
\text{0.0} 序
- 啊寄寄寄,我学圆锥曲线和导数有啥用!反正考试的时候时间不够第二问都直接摆烂!但又不想完全摆烂!啊,太乱了,感觉自己会但没有完全会,遇到题思路巨大乱,想到的做法很多压根就算不出来,真就应了那就话:
> 题题有思路,路路行不通。
- 圆锥曲线一大堆结论搞得有点乱,想开一篇文章记录并证明一下,纪念自己曾经高考前会过一点点,并且补充一些圆锥曲线在平面几何中的优美结论。
- $\text{P.S.}$ 可能记录有一些有意思的题,不过高中圆锥曲线大部分题就是带套路找方法然后爆算(~~暴论~~),很难有有意思的题。
- 本文章主要以解析几何的形式进行数学计算和分析,平面几何的证明和分析应该只占据很少一部分。
- 写这篇博客固然将会浪费很多时间(~~就算不写也去摸鱼了啊喂~~),但也算是空闲时间精神上的一个支柱了吧,至少可以让自己少颓废一些。
# $\text{1.0}$ 圆
# $\text{2.0}$ 椭圆
## $\text{2.1}$ 第一定义
- 平面内与两个不重合的定点 $F_1 , F_2$ 的距离之和等于常数 $2a(2a>|F_1F_2|)$ 的点的轨迹称为椭圆。
即椭圆上的任意一点 $P$ 满足 $|PF_1| + |PF_2| = 2a$ 。
一般地,规定线段 $F_1F_2$ 的距离为 $2c$ 。
## $\text{2.2}$ 标准方程
根据椭圆的第一定义,以线段 $F_1F_2$ 的中点为坐标原点 $O$ ,以平行于 $F_1F_2$ 和垂直于 $F_1F_2$ 的方向建立平面直角坐标系,令 $F_1$ 是横坐标较小的一点,则有 $F_1(-c,0) , F_2(c,0)$,设椭圆上任意一点 $P(x,y)$ ,于是有
$$
\begin{aligned}
\sqrt{(x + c)^{2} + y^{2}} + \sqrt{(x - c)^{2} + y^{2}} = 2a
\end{aligned}
$$
考虑利用共轭根式的方法消元,两边同时乘 $\sqrt{(x+c)^{2} + y^{2}} - \sqrt{(x-c)^{2} + y^{2}}$ 后整理得
$$
\begin{aligned}
\sqrt{(x+c)^{2} + y^{2}} - \sqrt{(x-c)^{2} + y^{2}} = \frac{2cx}{a}
\end{aligned}
$$
由上述两式相加得
$$
\begin{aligned}
a + \frac{cx}{a} = \sqrt{(x+c)^{2} + y^{2}} \\
a^{2} + \frac{c^{2}x^{2}}{a^{2}} + 2cx = (x+c)^{2} + y^{2} \\
\frac{x^{2}}{a^{2}} + \frac{y^{2}}{a^{2} - c^{2}} = 1
\end{aligned}
$$
由于看起来不太简洁,一般地,规定 $b^2 = a^{2} - c^{2}$ ,于是我们得到椭圆的标准方程
$$
\begin{aligned}
\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^2} = 1
\end{aligned}
$$
显然 $-a \le x \le a , -b \le y \le b , a > b > 0$ 。
**注:若无特殊说明,下文中所有未提及方程的椭圆,均默认其方程为 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ 且 $a > b > 0$ 。**
## $\text{2.3}$ 形状
在追求严谨的数学上,我们要排除我们对于椭圆的刻板印象。
到目前为止,想想我们掌握了哪些关于椭圆的知识,仅仅是**椭圆的第一定义**和根据其推导出的**椭圆的标准方程**,根据这两者,我们只能直观地知道**椭圆是一条曲线**,我们甚至无法直观看出椭圆是一条闭合曲线,更不必说想当然地看出椭圆的形状。
先分别带入 $x = 0$ 和 $y = 0$ ,定义此时的点为顶点,我们得到四个顶点坐标 $A_1(-a,0) , A_2(a,0),B_1(0,b),B_2(0,-b)$ 。
考虑通过隐函数求导来确定其大致形状,于是我们对椭圆的标准方程两边同时进行对 $x,y$ 的微分,有
$$
\begin{aligned}
\text{d}\frac{x^{2}}{a^{2}} + \text{d} \frac{y^2}{b^{2}} = 0 \\
\frac{2x \cdot \text{d}x}{a^{2}} + \frac{2y \cdot \text{d}y}{b^{2}} = 0 \\
\frac{\text{d}y}{\text{d}x} = - \frac{b^{2}x}{a^{2}y}
\end{aligned}
$$
而这个 $\frac{\text{d}y}{\text{d}x}$ 就是几何意义上的切线斜率,所以过椭圆上任意一点 $P(x_{0},y_{0})$ 的切线斜率为 $-\frac{b^{2}x_0}{a^{2}y_0}$ 。
我们发现在第一象限,$x$ 从 $0$ 到 $a$ ,切线斜率为负,绝对值逐渐增大,在 $x$ 趋近于 $a$ 时斜率趋近于负无穷,故椭圆在第一象限的形状**呈外凸状**,且 $B_1(0,b)$ 和 $A_2(a,0)$ 分别是纵坐标和横坐标最大的点。
通过标准方程,不难看出椭圆是关于 $x$ 轴和 $y$ 轴还有坐标原点对称的,所以**椭圆在一、二、三、四象限都呈外凸状,且四个顶点分别是横坐标最大和最小,纵坐标最大和最小的点**,如下图。
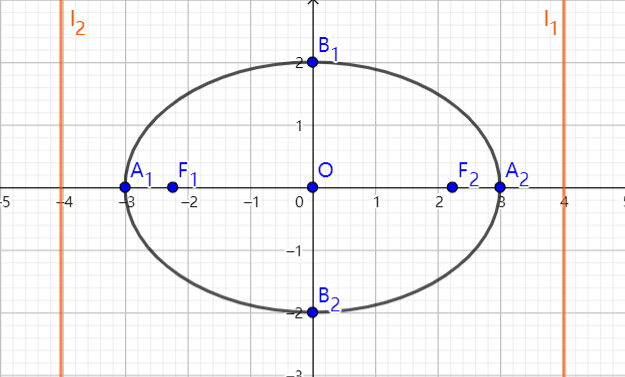
与此同时,我们还顺便得到了过椭圆上一点 $P(x_0 , y_0)$ 的切线方程
$$
\begin{aligned}
y = -\frac{b^{2}x_0}{a^{2}y_0}(x-x_0)+y_0
\end{aligned}
$$
整理得
$$
\frac{x_{0}x}{a^{2}} + \frac{y_{0}y}{b^{2}} = 1
$$
## $\text{2.4}$ 第二定义
- 平面上到定点 $F$ 与到定直线 $l(F\notin l)$ 的距离之比为定值 $e(0 < e < 1)$ 的点的轨迹为椭圆。
一般地,定义 $l$ 为椭圆的一条准线,定值 $e$ 为椭圆的离心率。
可以推出,$F$ 为椭圆靠近这条准线 $l$ 一侧的焦点。
### 证明
建立平面直角坐标系,设椭圆 $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ ,则其右焦点 $F_2(c,0)$ ,令直线 $l_2 : x = \frac{a^{2}}{c}$ 。
设椭圆上一点 $P(x_0,y_0)$ ,则有
$$
\begin{aligned}
|PF_{2}|^{2} = &\text{ } (x_{0} - c)^{2} + y_{0}^{2} \\
=&\text{ } x_{0}^{2} - 2cx_{0} + c^{2} + y_{0}^{2} \\
=&\text{ } \frac{c^{2}}{a^{2}}\left( \frac{a^{2}}{c^{2}} x_{0}^{2} - \frac{2a^{2}x_{0}}{c} + a^{2} + \frac{a^{2}}{c^{2}} y_{0}^{2} \right)
\end{aligned}
$$
因为
$$
\begin{aligned}
y_{0}^{2} = b^{2} - \frac{b^{2}x_{0}^{2}}{a^{2}}
\end{aligned}
$$
带入得
$$
\begin{aligned}
|PF_{2}|^{2}
=\text{ }& \frac{c^{2}}{a^{2}}\left(x_{0}^{2} - \frac{2a^{2}x_{0}}{c} + \frac{a^{2}(b^{2}+c^{2})}{c^{2}} \right) \\
=\text{ }& \frac{c^{2}}{a^{2}}\left(x_{0} - \frac{a^{2}}{c} \right)^{2} \\
=\text{ }& \frac{c^{2}}{a^{2}}\operatorname{d}(P,l_{2})^{2}
\end{aligned}
$$
两边同时开平方得
$$
\begin{aligned}
|PF_{2}| =\text{ }& \frac{c}{a}\operatorname{d}(P,l_{2})
\end{aligned}
$$
其中 $\operatorname{d}(P,l_{2})$ 表示点 $P$ 到直线 $l_{2}$ 的距离。(由于椭圆的对称性,对于左侧的准线和焦点也同理。)
所以我们推出了对于椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ ,离心率 $e = \frac{c}{a}$ ,准线 $l : x = \pm \frac{a^{2}}{c}$ 。
同时我们发现 $e = \sqrt{\frac{c^2}{a^{2}}} = \sqrt{1 - \frac{b^{2}}{a^{2}}}$ ,椭圆越扁,离心率越大。
### 推论(焦半径公式)
定义椭圆上一点 $P$ 到其中一个焦点的线段为椭圆的一条**焦半径**。
显然,一个椭圆有无数条焦半径,且不同的焦半径不一定等长。
设椭圆上一点 $P(x_0,y_0)$ ,$F_1(-c , 0)$ 为左焦点,$F_2(c,0)$ 为右焦点,根据椭圆的第二定义,则有焦半径
$$
\begin{aligned}
& |PF_1| = e ( x_{0} + \frac{a^{2}}{c} ) = a + ex_{0} \\
& |PF_2| = e ( \frac{a^{2}}{c} - x_{0} ) = a - ex_{0} \\
\end{aligned}
$$
若 $A(x_1,y_1) , B(x_2,y_2)$ 为椭圆上两点,且弦 $AB$ 过椭圆的左焦点 $F_1$ ,则 $|AB| = |AF_1| + |BF_1| = 2a + e(x_1 + x_2)$ 。
若 $A(x_1,y_1) , B(x_2,y_2)$ 为椭圆上两点,且弦 $AB$ 过椭圆的右焦点 $F_2$ ,则 $|AB| = |AF_2| + |BF_2| = 2a - e(x_1 + x_2)$ 。
## $\text{2.5}$ 直线与椭圆
> 我愿称之为万恶之源。
### 推论 $\text{1}
- 过原点的直线交椭圆于 A,B 两点,P 是椭圆上异于 A,B 的任意一点,当 k_{PA} 和 k_{PB} 都存在时 ,有 k_{PA} \cdot k_{PB} = -\frac{b^{2}}{a^{2}} 。
设 P(x_0 , y_0) , A(x_1,y_1) , B(-x_1 , -y_1) ,则有
\begin{aligned}
k_{PA} \cdot k_{PB} = \frac{y_0 - y_1}{x_0 - x_1} \cdot \frac{y_0 + y_1}{x_0 + x_1} =\frac{y_{0}^{2} - y_{1}^{2}}{x_{0}^{2} - x_{1}^{2}} \\
\end{aligned}
根据椭圆的标准方程,有
\begin{aligned}
y_{0}^{2} = b^{2} - \frac{b^{2}}{a^{2}} x_{0}^{2} \\
y_{1}^{2} = b^{2} - \frac{b^{2}}{a^{2}} x_{1}^{2} \\
\end{aligned}
带入第一个等式得
\begin{aligned}
k_{PA} \cdot k_{PB} = \frac{- \frac{b^{2}}{a^{2}} x_{0}^{2} + \frac{b^{2}}{a^{2}} x_{1}^{2} }{x_{0}^{2} - x_{1}^{2}} = -\frac{b^{2}}{a^{2}} \\
\end{aligned}
如下图。
推论 \text{2}
设 A(x_1,y_1) , B(x_2,y_2) ,则 M(\frac{x_1 + x_2}{2} , \frac{y_1 + y_2}{2}) 。根据椭圆的标准方程有
\begin{aligned}
\frac{x_{1}^{2}}{a^{2}} + \frac{y_{1}^{2}}{b^{2}} = 1 \\
\frac{x_{2}^{2}}{a^{2}} + \frac{y_{2}^{2}}{b^{2}} = 1 \\
\end{aligned}
由上述两式相减得
\begin{aligned}
\frac{x_{1}^{2} - x_{2}^{2}}{a^{2}} = -\frac{y_{1}^{2} - y_{2}^{2}}{b^{2}} \\
\frac{\frac{(y_1 + y_2)}{2}(y_1 - y_2)}{\frac{(x_1 + x_2)}{2}(x_1 - x_2)} = -\frac{b^{2}}{a^{2}} \\
k_{OM} \cdot k_{AB} = -\frac{b^{2}}{a^{2}}
\end{aligned}
此外,我们可以利用推论 1 来证明。
延长 BO 交椭圆于点 D ,则 k_{AD} \cdot k_{AB} = -\frac{b^{2}}{a^{2}} 。
因为 O 为 BD 的中点,M 为 AB 的中点,所以 OM 是 \triangle ABD 的一条中位线,所以 OM\kern 0.56em/\kern -0.8em /\kern 0.56em AD ,k_{OM} = k_{AD}。
所以 k_{OM} \cdot k_{AB} = k_{AD} \cdot k_{AB} = -\frac{b^{2}}{a^{2}} ,如下图。
推论 \text{3}
- 椭圆上的点 P 与两焦点构成的 \triangle PF_{1}F_{2} 叫做焦点三角形。设 \angle F_{1}PF_{2} = \alpha ,则 \text{S}_{\triangle PF_{1}F_{2}} = b^{2} \tan\frac{\alpha}{2} 。
设 |PF_1| = m , |PF_2| = n ,则根据椭圆的第一定义,有 m+n = 2a 。由余弦定理,有 4c^{2} = m^{2} + n^{2} - 2mn\cos\alpha 。
根据椭圆的标准方程的定义,有
\begin{aligned}
b^{2} &= a^{2} - c^{2} \\
&= \frac{1}{4} (m+n)^{2} - \frac{1}{4}\left(m^{2} + n^{2} - 2mn\cos\alpha \right) \\
&= \frac{1}{2} mn(\cos\alpha+1) \\
\end{aligned}
因为含有两条边的乘积 mn ,故直接带入三角形面积公式,有
\begin{aligned}
\text{S}_{\triangle PF_{1}F_{2}}
&= \frac{1}{2} mn \sin \alpha \\
&= \frac{b^{2} \sin\alpha}{\cos\alpha + 1}\\
&= \frac{2 b^{2} \sin\frac{\alpha}{2}\cos\frac{\alpha}{2}}{2 \cos^{2}\frac{\alpha}{2} - 1 + 1} \\
&= b^{2} \tan\frac{\alpha}{2}
\end{aligned}
如下图。
常用技巧 \text{1}
- 优美地计算一条直线与椭圆的两个交点所在的弦的长度。
直线 l : y = kx + b 交椭圆 \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 于 A(x_{1},y_{1}) , B(x_{2} , y_{2}) 两点。
注意这里的 A,B 两点的坐标是未求解的,是 x_{1} , y_{1} , x_{2} , y_{2} 都是假设的,如果直接解就变成了联立爆算了,毫无优美可言。
考虑联立后用韦达定理,这样我们不需要爆算,就可以较为轻松地计算出 x_1 + x_2 , y_{1} + y_{2} , x_{1}x_{2} , y_{1}y_{2} ,但我们必须用这些东西表示出 |AB| 才行。
注意,我们知道了 x_{1} + x_{2} 和 x_{1}x_{2} ,这样我们就可以通过 (x_{1} - x_{2})^{2} = (x_{1} + x_{2})^{2} - 4x_{1}x_{2} 求出 |x_{1} - x_{2}|。
这样们有了两点的横坐标之差,那么利用勾股定理和斜率,就可以得到 |AB| = \sqrt{1 + k^{2}} |x_{1} - x_{2}| = \sqrt{(1+k^{2})\left((x_{1}+x_{2})^2 - 4x_{1}x_{2}\right)} 。
\text{2.6} 椭圆的光学性质
大道至简。
- 从椭圆的一个焦点发出的光,经过椭圆的反射一定会经过椭圆的另一个焦点。(这里所指的反射,满足光的反射定律)
换句话说,F_1 , F_2 分别为椭圆的左右焦点,对于椭圆上任意一点 P ,GH 为椭圆过点 P 的切线,即证明 \angle F_{1}PG = \angle F_{2}PH 。如下图。
运用以上讲解的知识,用解析几何去证明的方法有很多,但没太有意思。
这里讲解一种大道至简的不需要解析几何的优美反证法。
平面几何反证法
作焦点 F_2 关于切线 GH 的对称点 F'_{2} ,则 \angle F_{2}PH = \angle F'_{2}PH 。即证 \angle F_{1}PG = \angle F’_{2}PH ,即证 F_1 , P , F'_{2} 三点共线。
因为 P 点在椭圆上,所以 |F_{1}P| + |F_{2}P| = 2a 。(结论一)
易证,除点 P 外在直线 GH 上的任意一点 Q 满足 |F_{1}Q| + |F_{2}Q| > 2a 。(结论二)
假设 F_{1} , P , F'_{2} 三点不共线。
连接 F_1F'_{2} ,交直线 GH 于点 P' 。因为 F_{1} , P , F'_{2} 三点不共线,所以 |F_{1}P'| + |F_{2}P'| < |F_{1}P| + |F_{2}P| = 2a ,与结论二矛盾。
故假设不成立,F_{1} , P , F'_{2} 三点共线成立。
3.0 双曲线
与椭圆大同小异,大部分结论十分相似,于是略写一二。
\text{4.0} 抛物线