传染病控制 题解
基础不牢
·
·
题解
update 2019/11/8
非常感谢评论区提出的连边方式问题,修改版也贴评论区了。有人看不见,还在喷。现在更新一下:
修改版:https://www.luogu.org/paste/bc41ih5u
小蒟蒻很菜,就发个题解给大家看看。有些大佬要是实在不愿意看可以移步下一篇,就不用在这里发表什么害人不浅之类的言论了。
要是修改版还有什么问题,请直接私信或在评论区提出。我一定会更改的。
在此对题解出锅表示非常抱歉。
题目传送门
第一眼看到这个题目,好像正解不好想的样子。但是再看看数据范围...发现n的范围很小,只要打个暴力就好了。
思路
题目给出一棵树。第i步拆的一定是第i层与第i+1层之间的连边,否则不是最优(自行证明即可),所以可以暴力枚举每一次拆哪一个节点与上一个节点的连边。
把所有节点所在的层数存下来,一号点在第1层,枚举每一层的每个节点(由于1号节点已经被感染,从第二层开始搜索就可以了)
大概可分为以下几步:
-
存好一整棵树
-
把每一层的节点都存在一个数组里面
-
标记以i号节点为根节点的子树的节点个数
-
标记与回溯
-
暴力搜索
以下内容分开来讲,会了的可以跳过。
树的存储
关于多叉树的存储,这里介绍一种简单有效的方法。考虑如下代码:
struct Node
{
int father,child[maxn],number;
};
Node node[maxn];
$father$存父亲 ; $child[maxn]$存它所有的孩子 ; $number$是它孩子的个数。
由于数据范围很小,我们不用担心造成空间过多的浪费。
结构体构建完成之后,我们就可以在读入的同时把整棵树存好。
void Input(void)
{
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++)//初始化
{
node[i].number=0;
count[i]=1;
}
for(i=1;i<=m;i++)
{
scanf("%d%d",&x,&y);
if(x>y) swap(x,y);
node[y].father=x;
node[x].number++;
node[x].child[node[x].number]=y;
}
}
------------
## 标记深度
如果能够理解,标记深度是比较简单的。
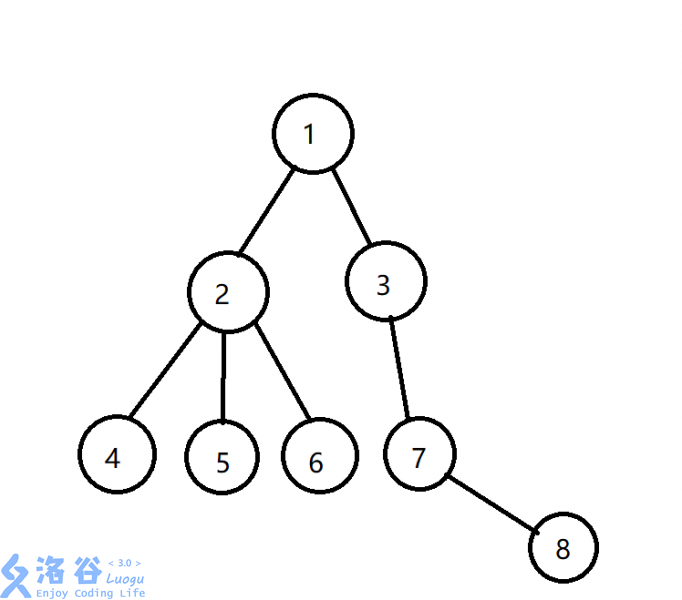
如图:我们令1号节点的深度为1 ; 则2,3节点深度为2 ; 4,5,6,7节点的深度为3 ; 8节点的深度为4。这棵树一共有4层。
代码用$deep[i][j]$存第$i$层第$j$个节点的编号。$deep[i][0]$是第$i$层一共的节点数。
void Deep(int tree,int now)//当前的节点标号是tree,层数是now
{
maxx=max(maxx,now);//标记一共有几层
for(int i=1;i<=node[tree].number;i++)
{
deep[now][0]++;//个数+1
deep[now][deep[now][0]]=node[tree].child[i];//把这个节点放到第i层的数组中
Deep(node[tree].child[i],now+1);//以这个点为父节点继续标记它的儿子。每个节点的深度等于它父节点的深度+1
}
return ;
}
------------
## 切断问题
我们知道,只要一个点与上层点的传播途径被切断,即这个点不会得传染病,那么以这个点为根节点的整个子树都应该被标记为安全。
这一段代码用来标记$tree$这个节点为根节点的子树一共有多少节点,存在$count[tree]$中。
int Count(int tree)
{
for(int i=1;i<=node[tree].number;i++)
{
count[tree]+=Count(node[tree].child[i]);
}
return count[tree];
}
接下来,我们切断了这个节点,相应地,以这个点为根节点的子树都应该被标记。(tag=1表示标记,tag=0表示删去标记,用于回溯)
void work(int tree,int tag)
{
for(int i=1;i<=node[tree].number;i++)
{
vis[node[tree].child[i]]=tag;//vis数组存标记
work(node[tree].child[i],tag);
}
return ;
}
------------
## 搜索
做完上面这些铺垫操作之后,我们可以开始整个代码的核心:搜索了。
首先可以想到如下代码
void dfs(int now,int cnt) //cnt是当前有多少个节点被感染,now是当前层数
{
if(now==maxx)//如果到了最后一层,更新答案
{
ans=min(ans,cnt);//如果感染人数小于答案,更新
return ;
}
for(int i=1;i<=deep[now][0];i++)//枚举这一层所有的节点
{
if(vis[deep[now][i]]>0)//如果该节点已经被标记为安全,直接跳过下面操作
continue;
vis[deep[now][i]]=1;//先标记这个节点
work(deep[now][i],1);//再标记它的子树
dfs(now+1,cnt-count[deep[now][i]]);//搜索下一层
vis[deep[now][i]]=0;//回溯,清除标记
work(deep[now][i],0);
}
}
但是提交这段代码的话只能得80分。为什么呢?
我们可以考虑这样一棵树:
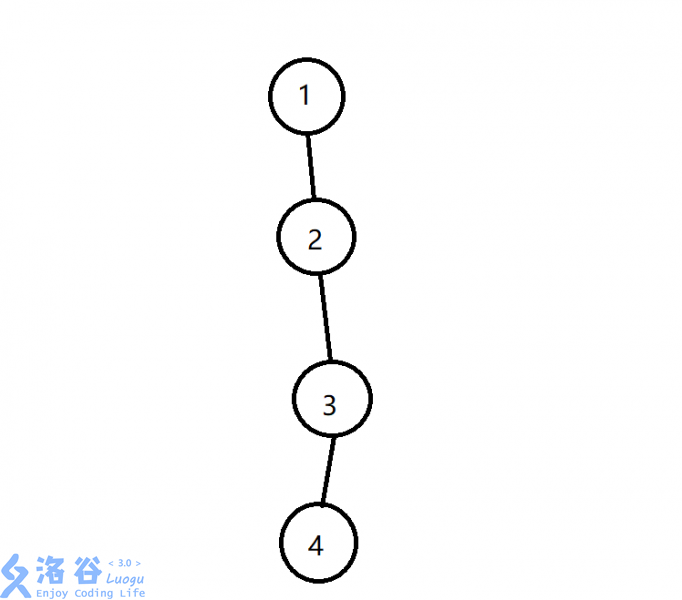
它是一条链。我们第一次只能切断1号节点和2号节点之间的连边,这样第三层所有的节点就都被标记了。那么问题是什么呢?根本就搜不到最后一层的节点,导致答案根本没有更新!
于是我们优化一下搜索代码:
void dfs(int now,int cnt)
{
if(now==maxx)
{
ans=min(ans,cnt);
return ;
}
int f=0;//制作一个标记
for(int i=1;i<=deep[now][0];i++)
{
if(vis[deep[now][i]]>0)
{
f++;//如果当前节点被标记,f+1
continue;
}
vis[deep[now][i]]=1;
work(deep[now][i],1);
dfs(now+1,cnt-count[deep[now][i]]);
vis[deep[now][i]]=0;
work(deep[now][i],0);
}
if(f==deep[now][0]) ans=min(ans,cnt);//如果这一层所有的节点都被标记了,直接更新答案。
}
这样,这道题就被完美地解决了。
上~~高清无注释方便复制的~~代码(不用o2 293ms 食用o2 106ms,加快读可能更快一点)
#include<cstdio>
#include<cmath>
#include<iostream>
using namespace std;
const int maxn=500;
int vis[maxn],deep[maxn][maxn],count[maxn];
int n,m,i,j,x,y,ans=1006,maxx=0;
struct Node
{
int father,child[maxn],number;
};
Node node[maxn];
void Input(void)
{
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++)
{
node[i].number=0;
count[i]=1;
}
for(i=1;i<=m;i++)
{
scanf("%d%d",&x,&y);
if(x>y) swap(x,y);
node[y].father=x;
node[x].number++;
node[x].child[node[x].number]=y;
}
}
void Deep(int tree,int now)
{
maxx=max(maxx,now);
for(int i=1;i<=node[tree].number;i++)
{
deep[now][0]++;
deep[now][deep[now][0]]=node[tree].child[i];
Deep(node[tree].child[i],now+1);
}
return ;
}
int Count(int tree)
{
for(int i=1;i<=node[tree].number;i++)
{
count[tree]+=Count(node[tree].child[i]);
}
return count[tree];
}
void work(int tree,int tag)
{
for(int i=1;i<=node[tree].number;i++)
{
vis[node[tree].child[i]]=tag;
work(node[tree].child[i],tag);
}
return ;
}
void dfs(int now,int cnt)
{
if(now==maxx)
{
ans=min(ans,cnt);
return ;
}
int f=0;
for(int i=1;i<=deep[now][0];i++)
{
if(vis[deep[now][i]]>0)
{
f++;
continue;
}
vis[deep[now][i]]=1;
work(deep[now][i],1);
dfs(now+1,cnt-count[deep[now][i]]);
vis[deep[now][i]]=0;
work(deep[now][i],0);
}
if(f==deep[now][0]) ans=min(ans,cnt);
}
int main()
{
Input();
Deep(1,2);
Count(1);
dfs(2,n);
printf("%d",ans);
return 0;
}
### 如果觉得有收获,就点个赞呗~