期望的线性性总结
Euler_Pursuer
·
2022-05-06 09:46:39
·
个人记录
今天做了一个 CF 的 Gym 题,遇到了 Harsh Comments 这道期望题,重新审视了自己对概率与期望的了解程度,发现这里问题还不小,有必要写下这篇总结报告。从浅入深,挑战最终的期望大 Boss!
期望的线性性
形式化定义就是:两个或多个随机变量的和之期望等于它们期望之和,也即
E(\sum_iX_i)=\sum_iE(X_i)
单纯看这个是没有什么眉目的,所以我们需要具象化。
典型问题
骰子问题
投掷一个均匀骰子的点数期望我们知道是 E(X)=3.5 ,那么投掷两个骰子呢?如果我们采用传统的枚举方法,很显然会枚举到头晕,事实上用期望表示就是 E(X+X)=7 。更多骰子就同理了。
饮料问题
咖啡馆里,一个心不在焉的女服务员拿来十杯饮料,要分别分给十个顾客。但是她忘记了谁点的哪个饮料,所以决定随机分配,请问分配正确人数的期望是多少?
我们不难知道,对于一个顾客来说,分配正确的期望是 E(X_i)=0.1 ,那么十位顾客分配正确的人数期望就是 E(\sum_i X_i)=\sum_i E(X_i)=10\times 0.1= 1 了。
点菜问题
六位顾客点四样菜,并且他们之间没有交流,那么没有被点到的菜期望有多少呢?
一道菜没有任何顾客选中很好得到:E(X_i)=(\frac{3}{4})^6 ,那么四道菜就是 4E(X_i)\approx 0.7 。
要注意的是,这里定义的指标变量 X_i 指代的是,如果没有任何人选这道菜,那么它将赋值为 1 ,代表没有选中它。
进阶问题
拓扑图问题
给定一个拓扑图,从一个点离开的 k 条边中,有 \frac{1}{k} 等概率选择一条边离开。求起点到终点的期望路径长度。
我们不难知道,这个期望就等于每条边的期望经过次数乘上它们各自的权值,那么问题就变成如何求一条边的期望经过次数。而一条边的期望经过次数可以转化为求它出发点的期望经过次数再乘上 \frac{1}{k} ,从而进一步将问题转化为求每个点的期望经过次数。我们会发现这是边和点期望经过次数相辅相成的问题。
对此我们可以利用拓扑排序,然后用递推关系进行求解,最后递推完毕后遍历所有边,将它们的次数期望乘上长度,就得到了最终的期望路径长度。
石子问题
这个基础问题是我们挑战最终 Boss 的关键,也是期望线性性的很好深入,务必吃透。
题目给定 n\le 10^5 堆石子,每堆石子有 a_i 颗石子,每次等概率选择一颗 石子,然后一次性取完它这堆的所有石子(后面这堆石子就不纳入概率考虑内)。请你求出第 1 堆石子被取走时的次数期望。
我们设第 i 堆石子被取走的次数为随机变量 t_i ,我们要求的次数设为随机变量 T ,满足:
T=1+\sum_i[t_i<t_1]
要求的期望就是:
E(T)=1+E(\sum_i[t_i<t_1])
这里就可以用到期望的线性性了:我们可以将 [t_i<t_1] 视作新的随机变量。于是就得到:
E(T)=1+\sum_iE([t_i<t_1])
因此我们仅需对一个 i 考虑如何求 E([t_i<t_1]) 即可,考虑谁先被选,我们不难得到:
E([t_i<t_1])=\dfrac{a_i}{a_1+a_i}\times 1+\dfrac{a_1}{a_1+a_i}\times 0
=\dfrac{a_i}{a_1+a_i}
所以将这些期望求和就得到最终结果了。
棋盘问题
这是 TCO2013 的一道题。
给定一个 n\times n (2\le n )棋盘,其中的骑士 (类似于象棋的马 )一次可以同时横着走 a 格,竖着走 b 格;或者横着走 b 格,竖着走 a 格。对于一个格子能被攻击到 定义为:该格子被骑士占用,或者能够被某个骑士一次 走到。
现在在棋盘上的两个不同位置放置两个骑士,求期望被攻击到的格子个数。数据范围均为 10^9 。
面对如此庞大的数据范围,我们还是单考虑某一个格子,假设它可以被攻击到的格子个数为 w ,那么我们可以得到这个格子处于被攻击状态时的概率为:
P=\dfrac{n^2\times(n^2-1)-(n^2-w)\times(n^2-w-1)}{n^2\times(n^2-1)}
那么它的期望贡献在数值上是和它相等的:
E(X)=P
根据期望的线性性,我们将所有这些格子的期望贡献求和就能得到答案。不过需要解决的就是:每个格子的 w 不尽相同,所以这里需要稍微处理一下。我们发现发生 w 变化的数值集合为 \{0,a,b,n-a,n-b,n\} ,可能根据处理方式不同会有 \pm 1 的差别。所以我们将区域划分出来,然后分别处理一下,最后再求和即可。
点名问题
在优化方案前,每个人都要被点一次名,所以期望就是 $n$。而后来的方案中,一个人要被点到,必须要满足它的所有死亡祖先在排列中是在它后面的。我们考虑它有 $k$ 个死亡祖先,就有 $k!$ 种排列,而剩下的 $n-k-1$ 个节点也有 $(n-k-1)!$ 种排列。然后考虑插入,就是 $C_{n}^{k+1}$,最后乘起来除去总方案数 $n!$ 得到被点名概率(期望):$E(X)=\frac{1}{k+1}$。
所以我们只需遍历一遍,寻找每个节点的死亡祖先个数,得到每个节点的点名次数期望。根据期望的线性性,累加求和即可得到新方案的点名期望次数,最后用 $n$ 减去它即可。
## 折枝问题
有一棵 $n\le 10^5$ 节点的树,每次随机选一个未删除的节点,删除它以及它的子树中的所有节点。当树为空时,期望经过了多少次删除操作呢?
乍一看,好像一个节点被删掉的概率是 $\frac{d_i}{n}$,其中 $d_i$ 表示点 $i$ 的深度。但是我们会注意到其中一衣带水的关系,关键是分母也会发生改变,这就使得我们的计算变得很麻烦。
如果我们着眼于“次数”这个关键词呢?可能现在还很抽象,我们举例子。
### $n=1$ 的链
显然期望为 $1$。
### $n=2$ 的链
期望是 $E(X)=1\times 0.5+2\times0.5=1.5$。
### $n=3$ 的链
- 选根节点时:$P(1)=\frac{1}{3}$,此后没有新选择;
- 选中间节点时:$P(2)=\frac{1}{3}$,此后选根节点就是 $P(1)=1$ 了;
- 选底节点时:$P(3)=\frac{1}{3}$,此后仍有两种选择:
- 选根节点:$P(1)=\frac{1}{2}$,此后没有新选择;
- 选中间节点:$P(2)=\frac{1}{2}$,此后选根节点就是 $P(1)=1$ 了。
总的来说,操作次数期望为:$E(X)=\frac{1}{3}+2\times(\frac{1}{3}+\frac{1}{3}\times\frac{1}{2})+3\times\frac{1}{3}\times \frac{1}{2}=\frac{1}{3}+1+\frac{1}{2}=\frac{11}{6}$。这里我们看清一下每个节点贡献了啥:
- 根节点:$\dfrac{1}{3}+\dfrac{1}{3}+\dfrac{1}{6}+\dfrac{1}{6}=1$;
- 中间节点:$\dfrac{1}{3}+\dfrac{1}{6}=\dfrac{1}{2}$;
- 底节点:$\dfrac{1}{6}+\dfrac{1}{6}=\dfrac{1}{3}$。
我们发现它们对次数产生的贡献等于它们节点深度的倒数!这是为什么呢?我们以一个节点来看,它自己被删除的时候必然发生在它自身或者它的祖先被删除的时候。也就是我们指定一个指标 $X_i$,当它发生删除时有 $X_i=1$,而其它情况就是 $X_i=0$。
我们对于会变化的概率比较难以确定,我们可以让选择依然保持在 $n$ 个节点范围,只不过被删除的节点不会对次数产生增加。产生次数贡献的指标为 $X_i=1$ 时当且仅当 $i$ 及其祖先均未被选中时!我们可以考虑某次选择时, $i$ 及其祖先还未被选中,那么 $E(X_i)$ 就应当表示为其祖先未被选中的情况下,它本身被选中的概率。又或者说,**在选中它以及它祖先的条件下,选择到它产生的贡献**,因此 $E(X_i)=\dfrac{1}{d_i}$!
换个角度,如果我们压根没选这条链,也就是说此时事件还未发生,我们就不考虑贡献。事件发生的前提条件是**它或者它的祖先被选中**,而事件中导致贡献的产生是**恰好**选中了它,根据条件期望我们就得到了那个式子。但是如果已经考虑完了,后面的事件也就不会再次落到这里,因此也视为事件不发生。
这就解释清楚了次数贡献期望对于一个节点来说是什么,从而我们就可以使用期望的线性性,求和所有节点的期望计算得到最终答案:
$$
E(\sum_iX_i)=\sum_iE(X_i)=\sum_i \dfrac{1}{d_i}
$$
# 提高问题
## 分治计数问题
给定一棵 $n\le 1000$ 节点的基环树,设 $t=0$,每次不断对**每一个**连通分量执行如下操作:
- 对 $t$ 加上连通分量的节点数;
- 在连通分量内随机选择一个节点进行删除(包括其连接的边)。
无独有偶,这里我们也需要着眼于每个点产生的贡献。但是注意到每次 $t$ 增加的数目和整个连通块的节点个数有关,这就让我们有些为难了。
其实,这里确实是着眼于每个节点产生的贡献,只不过需要着眼于的不是一个节点,而是节点对。因为我们可以考虑:当某一个节点被删除,之后它将不会产生任何贡献;那么在它删除时,我们记录的贡献是它所在连通块的节点总数。那么是不是我们就可以记录为这个节点与其它节点组成的节点对产生了 $1$ 的贡献呢?
### 基本分析
同时我们也注意到,这道题和上面的“折枝问题”的异曲同工之处:只有当节点对 $(u,v)$ 连通的时候才记录此贡献,而当它们之间简单路径唯一时(考虑环的后面再讨论),产生贡献的期望就是 $E[(u,v)]=\frac{1}{d}$,其中 $d$ 表示 $(u,v)$ 路径上的节点数(包括它们自身)。
为什么呢?同上题所述,只有当 $(u,v)$ 之间产生删除操作时才会发生计数事件,而 $(u,v)$ 节点对有效计数时,必须恰好处于 $u$ 节点被删除时(注意这就表明这里是有序对)。
### 考虑环
如果 $(u,v)$ 之间存在环呢?此时我们会发现,如果环上除 $(u,v)$ 路径上的“割点”之外的那些点被删去之后,$(u,v)$ 仍然连通,依然可以记录贡献。所以我们可以考虑两种情况:
- 第一次直接删的是 $u$ 节点;
- 第一次先删除不影响 $(u,v)$ 连通的节点,然后删除 $u$ 节点。
那么我们假设 $(u,v)$ 之间两条简单路径的并的总结点数为 $z$,其中一条简单路径节点数为 $x$,另一条为 $y$。那么产生贡献的期望就是:
$$
E[(u,v)]=\dfrac{1}{z}+\dfrac{z-x}{z}\cdot\dfrac{1}{x}+\dfrac{z-y}{z}\cdot\dfrac{1}{y}=\dfrac{1}{x}+\dfrac{1}{y}-\dfrac{1}{z}
$$
当然,我们还可以这样考虑:
- 只看一条路径时恰好删除的是 $u$;
- 同时看两条路径时恰好都删除了 $u$;
这里的意思是我们分别考虑这两条路径发生事件时的贡献期望,然后再减去重复的“同时删除“产生的贡献期望。如果我们假设 $u$ 到环上的路径节点数加上 $v$ 到环上的路径节点数为 $Z$,而环上除去”割点“之外的一个半环节点数为 $X$,另一半为 $Y$。那么此时产生的贡献期望就是:
$$
E[(u,v)]=\dfrac{1}{X+Z}+\dfrac{1}{Y+Z}-\dfrac{1}{X+Y+Z}
$$
如图我们显示了 $Z$ 为橙色点的个数,$X$ 为绿色点个数,$Y$ 为蓝色点个数。
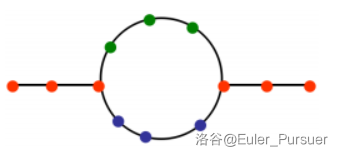
简单对比上述两式,会发现它们是一样的。不过第一个式子表示的意义更容易弄懂。
那么对于两两点对之间的距离,我们可以将环看作根节点集合,然后挂着许多树。据此用 $O(n^2)$ 处理出我们所需要的点对贡献,最后将它们加起来就得到答案了。
## Harsh Comments
这是 OpenCup XXI 的一道题,重新审视其实并不难。
题目给定 $N$ 个你的评论,$M$ 个别人的评论。其中,你的第 $i$ 个评论有 $a_i$ 个差评,别人的第 $i$ 个评论有 $b_i$ 个差评。现在博主将一步步删掉这些评论,每一步都会根据当前剩余结论的所有差评数通过**加权**概率选取一个评论进行删除。请问你的评论被删完时,期望步数为多少。
事实上,这就是前面的石子问题的升级版罢了!
我们知道,如果没有任何别人的评论在我们前面删掉,那么我们固定是有 $N$ 步的。同样我们考虑某一个在我们评论前删掉的评论,其它评论和前面的石子问题一样,利用线性性就可以解决!
我们设如果这个别人的评论没有被删除时,我们还剩余的评论集合为 $T$,而我们的总评论集合为 $S$。如果那个人的评论在**恰好**这 $|T|$ 个评论前被删掉,就有:
$$
P_T(X_i)=\dfrac{b_i}{b_i+\sum_{a_j\in T}a_j}
$$
但是在计算期望时,不同于前,如果当前没有恰好删掉,那么它还会产生**后效影响**:
$$
E_T(X_i)=P_T(X_i)+(1-P_T(X_i))P_{T'}(X_i)+\cdots
$$
而这样的**后效影响**就决定了这道题不能单纯考虑一个子集对应的概率就是其期望,我们就需要重新审视。
### 再看石子问题
如果我们类似于石子问题那样,考虑第 $i$ 个别人的评论被取走的次数 $t_{bi}$,而我们的第 $j$ 个评论被取走的次数 $t_{aj}$,此时是否能考虑类似 $t_{bi}<t_{aj}$ 的情况数呢?
答案是可以,但是我们还需要考虑到 $t_{bi}<t_{aj_1},t_{aj_2},\cdots,t_{aj_r}$ 的多元情况。我们会发现,在考虑 $t_{bi}<t_{aj_1}$ 的时候,就内含了 $t_{bi}<t_{aj_1},t_{aj_2}$ 的情况,也内含了 $t_{bi}<t_{aj_1},t_{aj_3}$ 的情况等。
而我们可以对比石子问题,容易发现 $[t_{bi}<t_{aj_1},t_{aj_2},\cdots,t_{aj_r}]$ 的种种,都是**随机变量**,都遵循**期望的线性性**,而我们要考虑到恰好的 $[t_{aj_1},t_{aj_2},\cdots,t_{aj_l}<t_{bi}<t_{aj_{l+1}},t_{aj_{l+2}},\cdots,t_{aj_r}]$,就必须使用**容斥原理**,因为容斥原理就是让我们从**至少**转到**恰好**的有力工具!
而由于这道题的 $\sum a_i$ 并不大,所以可以利用背包方法进行容斥计算。如果遇到 $\sum a_i$ 比较大的问题,我们可以采用分治 $NTT$ 的方法计算,接下来一道题就是需要这样操作了。
## PKUWC2018 猎人杀
这道题也是类似上题的做法,不过在容斥的时候注意:考虑 $t_1<t_i$ 的容斥最后得到 $t_1$ 不在最后一个的结果,因此我们最后用 $1$ 再减去它即可。
而在求 $\sum_{S}(-1)^{|S|}$ 的时候,我们需要利用生成函数:$\prod_i(1-x^{w_i})$,利用分治 $NTT$ 快速计算即可。