两圆一线 & 两线一圆学习笔记
stripe_python
·
·
个人记录
前置知识
-
1 + 1 = 2
- 平面直角坐标系
- 直线的方程 y=kx+b
- 圆的标准方程 (x-a)^2+(y-b)^2=r^2
两线一圆
Description
在平面直角坐标系中,A(x_1, y_1), B(x_2, y_2)。现有一点 P(x, y),使 \triangle ABP 为直角三角形。 求 x, y 的关系。
Solution
过点 A 作 l_1 \bot AB 于点 A,过点 B 作 l_2 \bot BA 于点 B。
连接 AB。记 AB 的中点为点 C。以 C 为圆心,AC 长为半径画圆。
如图所示:
易证点 P 落在、且仅能落在 l_1, l_2, \text{圆} C 上。
Deduction
令 AB 的斜率 k^{'}=\dfrac{x_1-x_2}{y_1-y_2},则 l_1, l_2 的斜率 k = -\dfrac{1}{k^{'}} = -\dfrac{y_1-y_2}{x_1-x_2} = \dfrac{y_2-y_1}{x_1-x_2}。
设 l_1: y=kx+b_1,将点 A(x_1,y_1) 代入 y=kx+b_1 中,得
y_1=kx_1+b_1
解得 b_1=y_1-kx_1,即 l_1: y = k(x-x_1)+y_1。
同理可得 l_2: y = k(x-x_2)+y_2。
由中点坐标公式,点 C(\dfrac{x_1+x_2}{2}, \dfrac{y_1+y_2}{2})。
令 r^2=AC^2=(x_1-\dfrac{x_1+x_2}{2})^2+(y_1-\dfrac{y_1+y_2}{2})^2=\dfrac{(x_1-x_2)^2+(y_1-y_2)^2}{4}。
$$
(x-\dfrac{x_1-x_2}{2})^2+(y-\dfrac{y_1-y_2}{2}) = \dfrac{(x_1-x_2)^2+(y_1-y_2)^2}{4}
$$
## Conclusion
$x,y$ 满足:
$$
y = k(x-x_1)+y_1
\text{或} y = k(x-x_2)+y_2
\text{或} (x-\dfrac{x_1-x_2}{2})^2+(y-\dfrac{y_1-y_2}{2}) = \dfrac{(x_1-x_2)^2+(y_1-y_2)^2}{4}
$$
# 两圆一线
## Description
在平面直角坐标系中,$A(x_1, y_1), B(x_2, y_2)$。现有一点 $P(x, y)$,使 $\triangle ABP$ 为等腰三角形。 求 $x, y$ 的关系。
## Solution
连接 $AB$。以 $A$ 为圆心,$AB$ 长为半径画圆。以 $B$ 为圆心,$BA$ 长为半径画圆。
作 $AB$ 的垂直平分线 $l$。
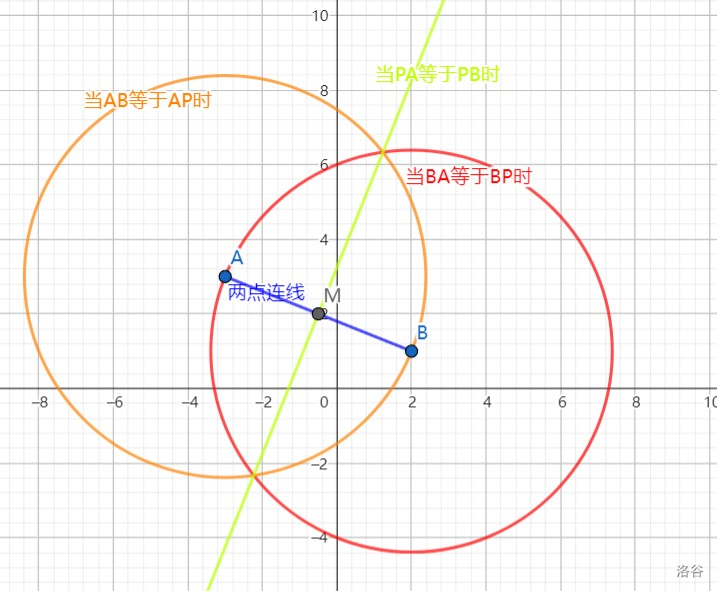
易证点 $P$ 落在、且仅能落在 $\text{圆} A, \text{圆} B, l$ 上。
## Deduction
令 $r^2 = AB^2 = (x_1-x_2)^2+(y_1-y_2)^2$。
则 $\text{圆} A: (x-x_1)^2+(y-y_1)^2 = r^2,\text{圆} B: (x-x_2)^2+(y-y_2)^2 = r^2
令 AB 的斜率 k^{'}=\dfrac{x_1-x_2}{y_1-y_2},则 l 的斜率 k = -\dfrac{1}{k^{'}} = -\dfrac{y_1-y_2}{x_1-x_2} = \dfrac{y_2-y_1}{x_1-x_2}。
设 l: y=kx+b。
同时,记 AB 的中点为点 M。
由中点坐标公式,点 M(\dfrac{x_1+x_2}{2}, \dfrac{y_1+y_2}{2})。
将 M(\dfrac{x_1+x_2}{2}, \dfrac{y_1+y_2}{2}) 代入 l: y=kx+b 中,得
\dfrac{y_1+y_2}{2} = \dfrac{x_1+x_2}{2}k+b
解得 b = \dfrac{y_1+y_2}{2}-\dfrac{x_1+x_2}{2}k。
所以 l: y = kx+\dfrac{y_1+y_2}{2}-\dfrac{x_1+x_2}{2}k。
Conclusion
$$
(x-x_1)^2+(y-y_1)^2 = (x_1-x_2)^2+(y_1-y_2)^2
\text{或} (x-x_2)^2+(y-y_2)^2 = (x_1-x_2)^2+(y_1-y_2)^2
\text{或} y = kx+\dfrac{y_1+y_2}{2}-\dfrac{x_1+x_2}{2}k
$$