线段树总结
noco
2018-10-10 21:54:16
# 线段树 Segment_Tree
树状数组解决一类具有交换律的问题
线段树则用来解决一类具有结合律的问题
这篇文章主要用来讲解简单的利用线段树维护的问题 其他知识点不定期update
## 一、关于线段树的结构
线段树其实本质上同样从分块衍生而来 实际上是**分块思想的树化** 以及二进制储存的思想
树形结构为什么具有如此的优秀性呢?
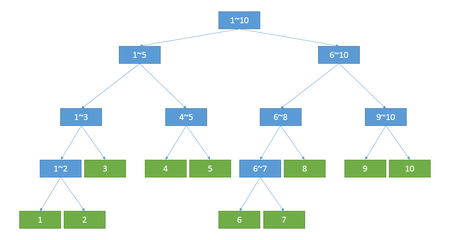
图片来源于互联网
首先由于是二叉树 树高是稳定log级别的 访问时则可以通过 因此每次传递信息都是log级的复杂度
其次是对于每一个子节点而言,它们都表示整个序列中的一段子区间;对于每个叶子节点而言,都表示序列中的单个元素信息;子节点不断向自己的父亲节点传递信息,而父节点存储的信息则是他的每一个子节点信息的整合。
但是呢重要的一点是**线段树并不能维护不具有区间结合律的信息** 而分块算法就十分优秀了嘛 而且就算$\sqrt n $时间复杂度的分块算法 其实大多数情况下还是跑不满的嘛 还是肥肠优秀的 所以呢大家还是有学习分块算法的必要的 毕竟 分块可以维护大多数的区间问题 比如区间众数
[分块入门](http://hzwer.com/8053.html)
## 二、线段树的构造与实现
### 1 储存
大多数情况下 我们会使用结构体来储存我们想要维护的信息
比如说
```cpp
struct segmentTree{
int l,r;
int sum,addtag;
int mul,multag;
int ma,mi;
}tr[N<<2];
```
如何通过父亲节点编号访问左右儿子呢?
```cpp
#define ls o<<1
#define rs o<<1|1
```
这样我们就可以十分方便的找到儿子啦!
### 2 维护
根据我们想要维护的信息我们就可以得到我们维护的代码啦
```cpp
inline void updateSum(int o){
tr[o].sum=tr[ls].sum+tr[rs].sum;
}
inline void updateMax(int o){
tr[o].ma=max(tr[ls].ma,tr[rs].ma);
}
inline void updateMin(int o){
tr[o].mi=min(tr[ls].mi,tr[rs].mi);
}
```
这一步update其实也就是合并左右儿子节点的信息来更新父亲节点的信息 也正是这样信息不断合并的过程需要我们维护的信息满足结合律啦QvQ
### 3 建树
对于建树,由于二叉树自身的父子节点之间的可传递关系,所以可以考虑递归建树 实际上呢 递归是自底向上的更新过程啦 由刚才的update操作也可以很清楚地明白为什么要递归建树
当然在这个过程中 我们还要顺便维护区间的信息( ̄▽ ̄)/
```cpp
void build(int o,int l,int r){
tr[o].l=l;
tr[o].r=r;
if(l==r){
tr[o].sum=a[l];
tr[o].ma=a[l]
tr[o].mi=a[l];
//......
return;
}
int mid=l+r>>1;
build(ls,l,mid);
build(rs,mid+1,r);
update(o);
}
```
### 4 区间修改
以下部分内容来自@皎月半洒花
为什么不讨论单点修改呢qwq?因为其实很显然,单点修改就是区间修改的一个子问题而已,即区间长度为1时进行的区间修改操作罢了qwq
那么对于区间操作,我们考虑引入一个名叫“lazytag”(懒标记)的东西——之所以称其“lazy”,是因为原本区间修改需要通过先改变叶子节点的值,然后不断地向上递归修改祖先节点直至到达根节点,时间复杂度最高可以到达$ O(nlogn) $的级别。但当我们引入了懒标记之后,区间更新的期望复杂度就降到了$O(logn)$的级别且甚至会更低.
**(1)首先先来从分块思想上解释如何区间修改:**
分块的思想是**通过将整个序列分为有穷个小块,对于要查询的一段区间,总是可以整合成k个所分块与m个单个元素的信息的并**$(0<=k,m<=logn)$
那么我们可以反过来思考这个问题:对于一个要修改的、长度为ll的区间来说,总是可以看做由一个长度为$ 2 ^ log(\lfloor{n})$和剩下的元素(或者小区间组成)。那么我们就可以先将其拆分成线段树上节点所示的区间,之后分开处理:
**如果单个元素被包含就只改变自己,如果整个区间被包含就修改整个区间**
其实好像这个在分块里不是特别简单地实现,但是在线段树里,无论是元素还是区间都是线段树上的一个节点,所以我们**不需要区分区间还是元**素,加个判断就好。
**(2)懒标记的正确打开方式**
首先,懒标记的作用是记录每次、每个节点要更新的值,但**线段树的优点不在于全记录(全记录依然很慢qwq),而在于传递式记录**:
**整个区间都被操作,记录在公共祖先节点上;只修改了一部分,那么就记录在这部分的公共祖先上;如果四环以内只修改了自己的话,那就只改变自己。**
这样以后,如果我们采用上述的优化方式的话,我们就需要在每次区间的查询修改时pushdown一次,以免重复或者冲突或者爆炸qwq
那么对于pushdown而言,其实就是纯粹的update的逆向思维(但不是逆向操作): 因为修改信息存在父节点上,所以要由父节点向下传导lazygtag
那么问题来了:怎么传导lazytag呢?这里很有意思,开始回溯时执行pushuppushup,因为是向上传导信息;那我们如果要让它向下更新,就调整顺序,在向下递归的时候pushdown不就好惹~qwq:
```cpp
//线段树1
inline void pushdown(int o){
if(tr[o].tag){
tr[ls].tag+=tr[o].tag;
tr[rs].tag+=tr[o].tag;
tr[ls].sum+=(tr[ls].r-tr[ls].l+1)*tr[o].tag;
tr[rs].sum+=(tr[rs].r-tr[rs].l+1)*tr[o].tag;
tr[o].tag=0;
}
}
void change(int o,int l,int r,ll v){
if(l<=tr[o].l&&tr[o].r<=r){
tr[o].sum+=(tr[o].r-tr[o].l+1)*v;
tr[o].tag+=v;
return;
}
int mid=tr[o].l+tr[o].r>>1;
pushdown(o);
if(l<=mid)change(ls,l,r,v);
if(r>mid)change(rs,l,r,v);
update(o);
}
```
当然我们还可以处理略微毒瘤一些的带有优先级的tag传递
```cpp
//线段树2
inline void pushdown(int o,int l,int r,int mid,int ls,int rs){
//mul
tr[ls].mul=(tr[ls].mul*tr[o].mul)%p;
tr[rs].mul=(tr[rs].mul*tr[o].mul)%p;
tr[ls].add=(tr[ls].add*tr[o].mul)%p;
tr[rs].add=(tr[rs].add*tr[o].mul)%p;
tr[ls].v=(tr[ls].v*tr[o].mul)%p;
tr[rs].v=(tr[rs].v*tr[o].mul)%p;
tr[o].mul=1;
//add
tr[ls].add=(tr[ls].add+tr[o].add)%p;
tr[rs].add=(tr[rs].add+tr[o].add)%p;
tr[ls].v=(tr[ls].v+tr[o].add*(mid-l+1))%p;
tr[rs].v=(tr[rs].v+tr[o].add*(r-mid))%p;
tr[o].add=0;
}
//mul
void change1(int o,int l,int r,int lc,int rc,ll k){
// if(rc<l||r<lc)return;
if(lc<=l&&r<=rc){
tr[o].mul=(tr[o].mul*k)%p;
tr[o].add=(tr[o].add*k)%p;
tr[o].v=(tr[o].v*k)%p;
return;
}
else{
int mid=l+r>>1;
if(tr[o].mul!=1||tr[o].add)pushdown(o,l,r,mid,ls,rs);
if(lc<=mid)change1(ls,l,mid,lc,rc,k);
if(rc>mid)change1(rs,mid+1,r,lc,rc,k);
tr[o].v=(tr[ls].v+tr[rs].v)%p;
}
}
//add
void change2(int o,int l,int r,int lc,int rc,ll k){
// if(rc<l||lc>r)return;
if(lc<=l&&r<=rc){
tr[o].add=(tr[o].add+k)%p;
tr[o].v=(tr[o].v+k*(r-l+1))%p;
return;
}else {
int mid=l+r>>1;
if(tr[o].mul!=1||tr[o].add)pushdown(o,l,r,mid,ls,rs);
if(lc<=mid)change2(ls,l,mid,lc,rc,k);
if(rc>mid)change2(rs,mid+1,r,lc,rc,k);
tr[o].v=(tr[ls].v+tr[rs].v)%p;
}
}
```
这里的tag**乘法优先**
对于复杂度而言,由于完全二叉树的深度不超过$logn$,那么单点修改显然是$O(logn)$的,区间修改的话,由于我们的这个区间至多分$logn$个子区间,对于每个子区间的查询是$O(1)$的,所以复杂度自然是$O(logn)$不过带一点常数~~而且常数还不小~~
### 5 区间查询
自然也是利用了分块的思想 二分的思想
```cpp
//线段树1
ll query(int o,int l,int r){
if(l<=tr[o].l&&tr[o].r<=r){
return tr[o].sum;
}
int mid=tr[o].l+tr[o].r>>1;
ll ret=0ll;
pushdown(o);
if(l<=mid)ret+=query(ls,l,r);
if(r>mid)ret+=query(rs,l,r);
return ret;
}
```
```cpp
//线段树2
ll query(int o,int l,int r,int lc,int rc){
// if(rc<l||lc>r)return 0;
if(lc<=l&&r<=rc)return tr[o].v%p;
else{
ll ans=0;
int mid=l+r>>1;
if(tr[o].mul!=1||tr[o].add)pushdown(o,l,r,mid,ls,rs);
if(lc<=mid)ans+=query(ls,l,mid,lc,rc);
if(rc>mid)ans+=query(rs,mid+1,r,lc,rc);
return ans%p;
}
}
```
线段树大法吼啊!(❁´ω`❁)
所以我还是贴上那两个模板题的代码吧
```cpp
//线段树1
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
#define ll long long
#define ls o<<1
#define rs o<<1|1
const int N=1e5+500;
int n,m;
ll a[N];
struct segmentTree{
int l,r;
ll sum,tag;
}tr[N<<2];
inline void update(int o){
tr[o].sum=tr[ls].sum+tr[rs].sum;
}
inline void pushdown(int o){
if(tr[o].tag){
tr[ls].tag+=tr[o].tag;
tr[rs].tag+=tr[o].tag;
tr[ls].sum+=(tr[ls].r-tr[ls].l+1)*tr[o].tag;
tr[rs].sum+=(tr[rs].r-tr[rs].l+1)*tr[o].tag;
tr[o].tag=0;
}
}
void build(int o,int l,int r){
tr[o].l=l;
tr[o].r=r;
if(l==r){
tr[o].sum=a[l];
return;
}
int mid=l+r>>1;
build(ls,l,mid);
build(rs,mid+1,r);
update(o);
}
void change(int o,int l,int r,ll v){
if(l<=tr[o].l&&tr[o].r<=r){
tr[o].sum+=(tr[o].r-tr[o].l+1)*v;
tr[o].tag+=v;
return;
}
int mid=tr[o].l+tr[o].r>>1;
pushdown(o);
if(l<=mid)change(ls,l,r,v);
if(r>mid)change(rs,l,r,v);
update(o);
}
ll query(int o,int l,int r){
if(l<=tr[o].l&&tr[o].r<=r){
return tr[o].sum;
}
int mid=tr[o].l+tr[o].r>>1;
ll ret=0ll;
pushdown(o);
if(l<=mid)ret+=query(ls,l,r);
if(r>mid)ret+=query(rs,l,r);
return ret;
}
int main(){
scanf("%d%d",&n,&m);
for(register int i=1;i<=n;i++)scanf("%lld",&a[i]);
build(1,1,n);
int opt,x,y;
ll k;
for(register int i=1;i<=m;i++){
scanf("%d",&opt);
if(opt==1){
scanf("%d%d%lld",&x,&y,&k);
change(1,x,y,k);
}else{
scanf("%d%d",&x,&y);
printf("%lld\n",query(1,x,y));
}
}
return 0;
}
```
还有动态开点的二倍空间线段树
```cpp
#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=1e5+50;
const int root=1;
int n,m;
ll w[N];
int tcnt=root;
struct segtree{
int l,r,lc,rc;
ll sum,tag;
}tree[N*4];
inline void upd(int o){
tree[o].sum=tree[tree[o].lc].sum+tree[tree[o].rc].sum;
}
inline void pushdown(int o){
int lc=tree[o].lc,rc=tree[o].rc;
if(tree[o].tag){
tree[lc].tag+=tree[o].tag;
tree[lc].sum+=(tree[lc].r-tree[lc].l+1)*tree[o].tag;
tree[rc].tag+=tree[o].tag;
tree[rc].sum+=(tree[rc].r-tree[rc].l+1)*tree[o].tag;
tree[o].tag=0;
}
}
void buildtree(int o,int l,int r){
tree[o].l=l,tree[o].r=r;
if(l==r){
tree[o].sum=w[l];
return;
}
int mid=(l+r)>>1;
tree[o].lc=++tcnt;
buildtree(tree[o].lc,l,mid);
tree[o].rc=++tcnt;
buildtree(tree[o].rc,mid+1,r);
upd(o);
}
void chang(int o,int l,int r,ll v){
if(l<=tree[o].l&&tree[o].r<=r){
tree[o].tag+=v;
tree[o].sum+=(tree[o].r-tree[o].l+1)*v;
return;
}
pushdown(o);
int mid=(tree[o].l+tree[o].r)>>1;
if(l<=mid)chang(tree[o].lc,l,r,v);
if(r>mid)chang(tree[o].rc,l,r,v);
upd(o);
}
ll ask(int o,int l,int r){
if(l<=tree[o].l&&tree[o].r<=r)
return tree[o].sum;
pushdown(o);
ll res=0;
int mid=(tree[o].l+tree[o].r)>>1;
if(l<=mid)res+=ask(tree[o].lc,l,r);
if(r>mid)res+=ask(tree[o].rc,l,r);
return res;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%lld",&w[i]);
buildtree(root,1,n);
while(m--){
int qus,x,y;
scanf("%d%d%d",&qus,&x,&y);
if(qus==1){
ll z;
scanf("%lld",&z);
chang(root,x,y,z);
}
if(qus==2)printf("%lld\n",ask(root,x,y));
}
return 0;
}
```
```cpp
//线段树2
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
#define ll long long
#define ls o<<1
#define rs o<<1|1
const int N=1e5+500;
int n,m,p;
ll a[N];
struct segmentTree{
ll v;
ll add,mul;
}tr[N<<2];
inline void update(int o){
tr[o].v=(tr[ls].v+tr[rs].v)%p;
}
inline void pushdown(int o,int l,int r,int mid){
//mul
tr[ls].mul=(tr[ls].mul*tr[o].mul)%p;
tr[rs].mul=(tr[rs].mul*tr[o].mul)%p;
tr[ls].add=(tr[ls].add*tr[o].mul)%p;
tr[rs].add=(tr[rs].add*tr[o].mul)%p;
tr[ls].v=(tr[ls].v*tr[o].mul)%p;
tr[rs].v=(tr[rs].v*tr[o].mul)%p;
tr[o].mul=1;
//add
tr[ls].add=(tr[ls].add+tr[o].add)%p;
tr[rs].add=(tr[rs].add+tr[o].add)%p;
tr[ls].v=(tr[ls].v+tr[o].add*(mid-l+1))%p;
tr[rs].v=(tr[rs].v+tr[o].add*(r-mid))%p;
tr[o].add=0;
}
void build(int o,int l,int r){
tr[o].mul=1;
tr[o].add=0;
if(l==r){
tr[o].v=a[l];
return;
}
int mid=l+r>>1;
build(ls,l,mid);
build(rs,mid+1,r);
update(o);
}
void changeMul(int o,int l,int r,int lc,int rc,ll k){
if(lc<=l&&r<=rc){
tr[o].mul=(tr[o].mul*k)%p;
tr[o].add=(tr[o].add*k)%p;
tr[o].v=(tr[o].v*k)%p;
return;
}
int mid=l+r>>1;
if(tr[o].mul!=1||tr[o].add)
pushdown(o,l,r,mid);
if(lc<=mid)changeMul(ls,l,mid,lc,rc,k);
if(rc>mid)changeMul(rs,mid+1,r,lc,rc,k);
update(o);
}
void changeAdd(int o,int l,int r,int lc,int rc,ll k){
if(lc<=l&&r<=rc){
tr[o].add=(tr[o].add+k)%p;
tr[o].v=(tr[o].v+(r-l+1)*k)%p;
return;
}
int mid=l+r>>1;
if(tr[o].mul!=1||tr[o].add)
pushdown(o,l,r,mid);
if(lc<=mid)changeAdd(ls,l,mid,lc,rc,k);
if(rc>mid)changeAdd(rs,mid+1,r,lc,rc,k);
update(o);
}
ll query(int o,int l,int r,int lc,int rc){
if(lc<=l&&r<=rc)
return tr[o].v%p;
ll ret=0ll;
int mid=l+r>>1;
if(tr[o].mul!=1||tr[o].add)
pushdown(o,l,r,mid);
if(lc<=mid)ret+=query(ls,l,mid,lc,rc);
if(rc>mid)ret+=query(rs,mid+1,r,lc,rc);
return ret%p;
}
int main(){
scanf("%d%d%d",&n,&m,&p);
for(register int i=1;i<=n;i++)scanf("%lld",&a[i]);
build(1,1,n);
int opt,x,y;
ll k;
while(m--){
scanf("%d%d%d",&opt,&x,&y);
if(opt==1){
scanf("%lld",&k);
changeMul(1,1,n,x,y,k);
}else if(opt==2){
scanf("%lld",&k);
changeAdd(1,1,n,x,y,k);
}else {
printf("%lld\n",query(1,1,n,x,y));
}
}
return 0;
}
```
### 6 易错点
#### 1.ls和rs写反
#### 2.忘记在主函数中调用build函数
#### 3.不要#define mid l+r>>1
#### 4.特判中末尾要return
#### 5.l和lc写反 r和rc写反
以上智障错误的结果 大概使我RE或CE了无数次
在此记录