概率论之分布浅谈
andychen_2012
·
·
个人记录
本文目的
对概率论中常见分布进行整理与分析。
大部分来源于百度百科,oi-wiki,卡方分布、t分布、F分布的期望与方差的计算 以及 Dimitri P. Bertsekas, John N. Tsitsiklis 编著的《概率导论》一书。
目录
-
分布简析
-
离散分布
i. 0-1 分布(又称伯努利分布)
ii. 二项分布
iii. 泊松分布
iv. 几何分布
v. 超几何分布
vi. 负二项分布
-
连续分布
i. 均匀分布
ii. 指数分布
iii. 正态分布
iv. 标准正态分布
v. 伽马分布
-
抽样分布
i. 卡方分布
ii. t分布
iii. F分布
1. 分布简析
分布指示了一个随机变量的两重信息:
-
可以得到哪些值;
-
得到这些值的概率分别是多少(对离散变量而言,对连续随机变量是得到给定区间值的概率)
定义:设 X 是一个随机变量,x 为任意实数,则称函数 F(x)=P\{X \le x\} 为 X 的分布函数。有时也记为 X \sim F(x)。
可得 P\{x_1 \le x \le x_2\}=F(x_2)-F(x_1),其中两个 \le 都可以换成 <。又有 P\{x \ge x_1\}=1-F(x_1),其中 \ge 可以换成 >。
我们可以得到几个分布函数的基本性质:
-
分布函数不降性,也即对于任意 x_2>x_1,都有 F(x_2) \ge F(x_1)。
-
分布函数有界性,0 \le F(x) \le 1,F(-\infty)=0,F(+\infty)=1。
分布函数又称累积分布函数(英文缩写为 CDF),累积意味着 X 取值的概率由 -\infty 累计到 x。
在一个概率模型中,随机变量可以有不同的类型,可以是离散的,也可以是连续的,甚至可以是既非离散也非连续的。
但不管是什么类型的随机变量,它们有一个共同的特征,即都有一个分布函数,这是因为 \{X \le x\} 是一个随机事件,这些事件的概率形成概率分布。
今后,凡是刻画事件 \{X \le x\} 的概率的,都称为随机变量 X 的概率律。因此离散情况下的分布列,连续情况下的概率密度函数以及一般情况下的分布函数都是相应的随机变量的概率律。
顺便提一嘴概率中的期望和方差,这在分布中经常需要讨论。
离散型随机变量的期望定义:
设离散型随机变量 X 的概率分布为 p_i=P\{X=x_i\},若和式
\sum x_ip_i
绝对收敛,则称其值为 X 的期望,记作 E(X)。
连续型随机变量的期望定义:
设连续型随机变量 X 的密度函数为 f(x)。若积分
\int_{\Bbb{R}}xf(x)dx
绝对收敛,则称其值为 X 的期望,记作 E(X)。
有关期望的不等式有 Markov 不等式:
P\{X \ge a\} \le \frac{E(X)}{a}
方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望(即均值)之间的偏离程度。
离散型随机变量方差计算公式如下:
D(X)=E((X-E(X))^2)=E(X^2)-E^2(X)
**连续型随机变量**方差近似公式如下:
记连续型随机变量 $X$ 定义域为 $(a,b)$,概率密度函数为 $f(x)$,总体均值为 $\mu$,则有
$$
D(X)=\int(x-\mu)^2f(x)dx
$$
## 2. 离散分布
### i. 0-1 分布(又称伯努利分布)
结果仅有两种,$0$ 或 $1$。
| $x$ | $0$ | $1$ |
| :-----------: | :-----------: | :-----------: |
| $P\{X=x\}$ | $1-p$ | $p$ |
$E(X)=p$。
### ii. 二项分布
二项分布是 $n$ 个独立的成功/失败试验中成功的次数的离散概率分布,其中每次试验的成功概率为 $p$。
$n$ 次试验中正好得到 $k$ 次成功的概率由概率质量函数给出:
$$
P\{X=k\}={n \choose k}p^k(1-p)^{n-k}
$$
如果 $X \sim B(n,p)$(也就是说,$X$ 是服从二项分布的随机变量),那么 $X$ 的期望值为:
$$
E(X)=np
$$
### iii. 泊松分布
泊松分布的概率函数为:
$$
P\{X=k\}=\frac{\lambda^k}{k!}e^{-\lambda},k=0,1,\dots
$$
泊松分布的参数 $\lambda$ 是单位时间(或单位面积)内随机事件的平均发生次数。 泊松分布适合于描述单位时间内随机事件发生的次数。
泊松分布的期望和方差均为 $\lambda$。
### iv. 几何分布
定义:
1. 做某件事的次数是固定的,用 $n$ 表示,且 $n$ 次事件是相互独立的。
2. 每一件事件都有两个可能结果(成功 or 失败)
3. 每一次成功的概率都相等,成功的概率用 $p$ 表示
4. 想知道第 $k$ 次做某件事才取得成功的概率是多少(前 $k-1$ 次失败,第 $k$ 次成功)
因此我们有 $P(X=k)=(1-p)^{k-1}p,k=1,2,\dots$。
几何分布的期望为:
$$
E(X)=\frac{1}{p}
$$
### v. 超几何分布
超几何分布是统计学上一种离散概率分布。它描述了从有限 $N$ 个物件(其中包含 $M$ 个指定种类的物件)中抽出 $n$ 个物件,成功抽出该指定种类的物件的次数(不放回)。
产品抽样检查中经常遇到一类实际问题,假定在 $N$ 件产品中有 $M$ 件不合格品,即不合格率 $p=\frac{M}{N}$。
在产品中随机抽 $n$ 件做检查,发现 $k$ 件不合格品的概率为 $P(X=k)=\frac{{M \choose k}{N-M \choose n-k}}{{N \choose n}},k=0,1,2,\dots,\min(n,M)$。
需要注意的是:
(1)超几何分布的模型是不放回抽样。
(2)超几何分布中的参数是 $N,n,M$,上述超几何分布记作 $X \sim H(N,n,M)$。
超几何分布的期望和方差分别如下:
$$
E(X_i)=\frac{M}{N}
$$
$$
D(X_i)=\frac{M}{N}-\frac{M^2}{N^2}=\frac{M(N-M)}{N^2}
$$
$$
E(X)=\sum_{i=1}^n E(X_i)=\frac{nM}{N}
$$
$$
D(X)=\frac{nM(N-n)(N-M)}{N^2(N-1)}
$$
### vi. 负二项分布
满足以下条件的称为负二项分布:
1. 实验包含一系列独立的实验。
2. 每个实验都有成功、失败两种结果。
3. 成功的概率是恒定的,设为 $p$。
4. 实验持续到 $r$ 次失败,$r$ 可以为任意正数。
当 $r$ 为整数时,负二项分布又称帕斯卡分布,其概率质量函数为
$$
f(k;r,p)={k+r-1\choose r-1}p^r(1-p)^k
$$
它表示,已知一个事件在伯努利试验中每次的出现概率是 $p$,在一连串伯努利试验中,一件事件刚好在第 $r + k$ 次试验出现第 $r$ 次的概率。
参数为 $(r,p)$ 的负二项分布的数列 $k+r$ 的期望是 $\frac{rp}{1-p}$。
## 3. 连续分布
### i. 均匀分布
均匀分布由两个参数 $a$ 和 $b$ 定义,它们是数轴上的最小值和最大值,通常缩写为 $U(a,b)$。
均匀分布的概率密度函数为:
$$
f(x)=\frac{1}{b-a},a<x<b
$$
$$
f(x)=0,else
$$
在两个边界 $a$ 和 $b$ 处的 $f(x)$ 的值通常是不重要的,因为它们不改变任何 $f(x)dx$ 的积分值。
概率密度函数有时为 $0$,有时为 $\frac{1}{b-a}$。
其累积分布函数为:
$$
F(x)=0,x<a\\
F(x)=\frac{x-a}{b-a},a \le x \le b\\
F(x)=1,x>b
$$
因此我们可以求出其期望与方差:
$$
E(X)=\int_{-\infty}^{\infty}xf(x)dx=\frac{1}{b-a}xdx=\frac{a+b}{2}
$$
$$
E(X^2)=\int_a^b x^2\frac{1}{b-a}dx=\frac{b^3-a^3}{3(b-a)}=\frac{a^2+ab+b^2}{3}
$$
$$
D(X)=E(X^2)-(E(X))^2=\frac{a^2+ab+b^2}{3}-(\frac{a+b}{2})^2=\frac{(b-a)^2}{12}
$$
### ii. 指数分布

### iii. 正态分布
首先是一个重要的积分, 即**泊松积分**, 它在求有关正态分布的一些量时往往有强大的作用.
**引理1** 设 $a> 0 , b\in\mathbb{R}$ , 则
$\quad\int_0^{+\infty}e^{-ax^2}\cos bx\;\text{d}x=\frac12\sqrt{\frac\pi a}e^{-\frac{b^2}{4a}}
注记 (1). 特别地, 令 a=1 , b=0 可得
(2). 该引理可以利用留数定理证明。
定义2 若随机变量 \xi 有密度函数
\quad f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}
其中 \sigma>0 , \mu\in\mathbb{R} ; 则称 \xi 服从正态分布 N(\mu,\sigma^2) .
注记 (1). 要验证 p(x) 的确是一个密度函数, 只需要应用引理1即可.
(2). 正态分布的分布函数 \quad F(x)=\frac{1}{\sqrt{2\pi}\sigma}\int_{-\infty}^{x}e^{-\frac{(t-\mu)^2}{2\sigma^2}}\text{d}t 不是一个初等函数.
(3). 习惯上将服从正态分布的随机变量称为正态变量.
(4). 分布函数为 \chi_{(c,+\infty)} 的单点分布可以看作退化的正态分布 N(c,0) , 正态分布满足的性质退化分布也能算进来。
标准正态分布的密度函数一般记为
$\quad \varphi(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}
iv. 标准正态分布
当 \mu=0,\sigma=1 时,正态分布就成为标准正态分布:
f(x)=\frac{1}{\sqrt{2\pi}}e^{(-\frac{x^2}{2})}
v. 伽马分布
假设随机变量 X 为等到第 \alpha 件事发生所需之等候时间, 密度函数为
f(x,\beta,\alpha)=\frac{\beta^\alpha}{\Gamma(\alpha)}x^{\alpha-1}e^{-\beta x},x>0
因此我们有 E(X)=\frac{\alpha}{\beta},D(X)=\frac{\alpha}{\beta^2}。
4. 抽样分布
i. 卡方分布
若 n 个相互独立的随机变量 \xi_1,\xi_2,\dots,\xi_n ,均服从标准正态分布(也称独立同分布于标准正态分布),则这 n 个服从标准正态分布的随机变量的平方和 Q=\sum\limits_{i=1}^n\xi_i^2 构成一新的随机变量,其分布规律称为 \chi^2 分布(卡方分布),其中参数 n=v,称为自由度,记为 Q \sim \chi^2(n)。
则我们可得其期望为
E(X)=E(\sum_{i=1}^nX_i^2)=\sum_{i=1}^nE(X_i^2)=\sum_{i=1}^n(D(X_i)+E^2(X_i))
由 D(X_i)=1,E(X_i)=0,可得 E(X)=n。
其方差为
D(X)=D(\sum_{i=1}^nX_i^2)=\sum_{i=1}^nD(X_i^2)=\sum_{i=1}^n(E(X_i^4)-E^2(X_i^2))
由上可得 E(X_i^2)=1。
而
因此我们有 D(X_i^2)=3-1=2,则 D(X)=2n。
ii. t分布
由于在实际工作中,往往 \sigma 是未知的,常用 s 作为 \sigma 的估计值,为了与 u 变换区别,称为 t 变换,统计量 t 值的分布称为 t 分布。
假设 X 服从标准正态分布 N(0,1),Y 服从 \chi^2(n) 分布,那么 Z=\frac{X}{\sqrt{\frac{Y}{n}}} 分布称为自由度为 n 的 t 分布。
分布密度函数为 f_Z(x)=\frac{\Gamma(\frac{n+1}{2})}{\sqrt{n\pi}\Gamma(\frac{n}{2})}(1+\frac{x^2}{2})^{-\frac{n+1}{2}}。
期望计算如下:
E(T)=E(\frac{X_1}{\sqrt{\frac{X_2}{n}}})=nE(\frac{X_1}{\sqrt{X_2}})
由于 X_1,X_2 彼此独立,所以 E(\frac{X_1}{\sqrt{X_2}})=E(X_1)E(\frac{1}{\sqrt{X_2}})。
方差计算如下:
$$
D(T)=E(T^2)-E^2(T)=E(T^2)\\
E(T^2)=E(\frac{X_1^2}{\frac{X_2}{n}})=nE(\frac{X_1^2}{X_2})
$$
由于 $X_1,X_2$ 彼此独立,所以 $E(\frac{X_1^2}{X_2})=E(X_1^2)E(\frac{1}{X_2})$。
由于 $X_1 \sim N(0,1)$,所以 $E(X_1^2)=1$。
由于 $X_2 \sim \chi^2(n)$,所以
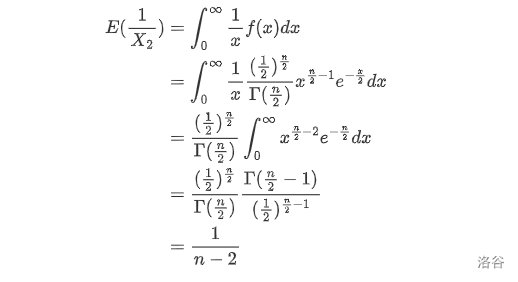
所以 $D(T)=E(T^2)=nE(X_1^2)E(\frac{1}{X_2})=\frac{n}{n-2}$。
### iii. F分布
若总体 $X \sim N(0,1)$,$(X_1,X_2,\dots,X_{n_1})$ 与 $(Y_1,Y_2,\dots,Y_{n_2})$ 为来自 $X$ 的两个独立样本,设统计量
$$
F=\frac{\sum\limits_{i=1}^{n_1}X_i^2}{n_1}/\frac{\sum\limits_{i=1}^{n_2}Y_i^2}{n_2},
$$
则称统计量 $F$ 服从自由度 $n_1$ 和 $n_2$ 的 F 分布,记为 $F \sim F(n_1,n_2)$。
其期望计算如下:
$$
E(F)=E(\frac{X/n_1}{Y/n_2})=\frac{n_2}{n_1}E(\frac{X}{Y})\\
\because X \sim \chi^2(n_1),Y \sim \chi^2(n_2),\text{X,Y 彼此独立}\\
\therefore E(\frac{X}{Y})=E(X)E(\frac{1}{Y})\\
E(X)=n_1,E(\frac{1}{Y})=\frac{1}{n_2-2}\\
\therefore E(F)=\frac{n_2}{n_1}E(\frac{X}{Y})=\frac{n_2}{n_2-2}
$$
其方差计算如下:
$$
E(F^2)=\frac{n_2^2}{n_1^2}E(\frac{X^2}{Y^2})\\
\because X_1 \sim \chi^2(n_1)\\
$$
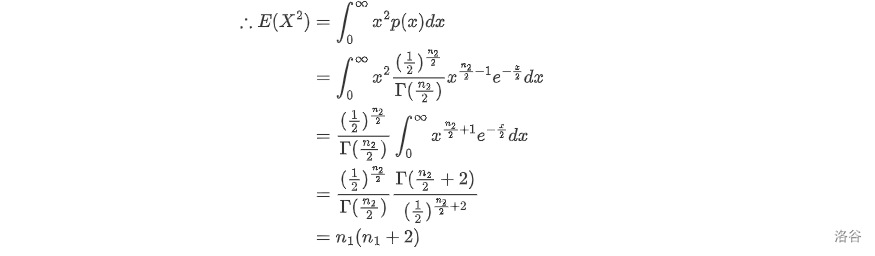
由于 $Y \sim \chi^2(n_2)$,所以我们有
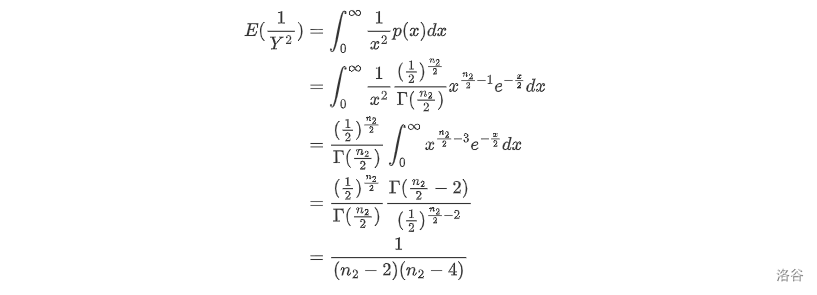
因此,$E(F^2)=\frac{n_2^2}{n_1^1}E(X^2)E(\frac{1}{Y^2})=\frac{n_2(n_1+2)}{n_1(n_2-2)(n_2-4)}$。
所以,$D(F)=E(F^2)-E(F)^2=\frac{2n_2^2(n_1+n_2-2)}{n_1(n_2-2)^2(n_2-4)}$。