【KX】百题大集结,超全联赛DP练习题目(入门篇)
king_xbz
2020-11-18 07:49:42
# 百题大集结,超全联赛DP练习题目(入门篇)
总结一下自己是如何训练自己最薄弱环节之一:DP。
本文与上文知识点内容相匹配哟!
## 前言
本文所有题目基本均选自洛谷,UVA,ATcoder,Codeforces,SPOJ,XDOJ等网站及NOI系列,USACO,各省省选,个人公开赛等相关比赛,均标明出处。个人学习用,无商业用途!
题目选择:这里都是一些相对基础的题目,难度在`普及-`到`提高+/省选-`不等。有些是基础的DP模型应用,也有状态转移比较难搞或者比较难以想到模型的题目。还是比较有价值的。
## 线性DP问题(73道)
#### [1,Number Triangles](https://www.luogu.com.cn/problem/P1216)
从下往上倒推还原$f_{i,j}=f_{i+1,j+1}+f_{i+1,j}$
```cpp
int main()
{
int n;
cin>>n;
for(fint i=1;i<=n;i++)
for(fint j=1;j<=i;j++)
cin>>f[i][j];
for(fint i=n-1;i>=1;i--)
for(fint j=1;j<=i;j++)
f[i][j]+=max(f[i+1][j+1],f[i+1][j]);
cout<<f[1][1];
return 0;
}
```
#### [2,采药](https://www.luogu.com.cn/problem/P1048)
DP方程(二维):$f_{i,j}=max(f_{i-1,j},f_{i-1,j-w_i}+v_i)$
然而会炸空间,所以压缩为一维。
$f_j=max(f_j,f_{j-w_i}+v_i)$
二维
```cpp
int main()
{
int n,m;
cin>>n>>m;
for(fint i=1;i<=m;i++)
cin>>tim[i]>>cost[i];
for(fint i=1;i<=m;i++)
for(fint j=n;j>=0;j--)
if(j>=tim[i])
f[i][j]=max(f[i-1][j],f[i-1][j-tim[i]]+cost[i]);
else
f[i][j]=f[i-1][j];
cout<<f[m][n];
return 0;
}
```
一维
```cpp
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=m;i++)
cin>>w[i]>>v[i];
for(int i=1;i<=m;i++)
for(int j=n;j>=w[i];j--)
f[j]=max(f[j],f[j-w[i]]+v[i]);
cout<<f[n];
return 0;
}
```
#### [3,导弹拦截](https://www.luogu.com.cn/problem/P1020)
$O(n^2)DP$:
$f_{i}=max(f_{i},f_{j}+1)$
```cpp
int main()
{
int cnt=0;
while(cin>>a[++cnt])
f[cnt]=1,dp[cnt]=1;
for(fint i=1;i<=cnt;i++)
for(fint j=1;j<i;j++)
if(a[j]>=a[i])
f[i]=max(f[i],f[j]+1);
int maxxs=0;
for(fint i=1;i<=cnt;i++)
maxxs=max(maxxs,f[i]);
cout<<maxxs-1<<endl;
for(fint i=1;i<=cnt;i++)
for(fint j=1;j<i;j++)
if(a[j]<a[i])
dp[i]=max(dp[i],dp[j]+1);
maxxs=0;
for(fint i=1;i<=cnt;i++)
maxxs=max(maxxs,dp[i]);
cout<<maxxs;
return 0;
}
```
**优化**
让f数组储存最大递增数列,若有比当前数列更大的就加入,否则二分查找这个数能否替换原序列的一个数(让序列中的一个数更小)
复杂度$O(nlogn)$
```cpp
f[1]=a[1];
int cnt=1;
for(fint i=2;i<=n;i++)
if(f[cnt]<=a[i])
f[++cnt]=a[i];
else
f[lower_bound(f+1,f+cnt+1,a[i])-f]=a[i];
```
#### [4,递增](https://www.luogu.com.cn/problem/P3902)
```cpp
int n;
cin>>n;
for(fint i=1;i<=n;i++)
cin>>a[i];
f[1]=a[1];
int cnt=1;
for(fint i=2;i<=n;i++)
if(f[cnt]<=a[i])
f[++cnt]=a[i];
else
f[lower_bound(f+1,f+cnt+1,a[i])-f]=a[i];
cout<<n-cnt;
```
#### [5,最长公共子序列](https://www.luogu.com.cn/problem/P1439)
$O(n^2)DP$:
$a_i=b_i\ 则 \ f_{i,j}=max(f_{i-1,j-1}+1,f_{i,j})$
$a_i!=b_i,f_{i,j}=max(f_{i-1,j},f_{i,j-1})$
```cpp
for(fint i=1;i<=n;i++)
for(fint j=1;j<=m;j++)
{
if(a[i]==b[j])
f[i][j]=max(f[i-1][j-1]+1,f[i][j]);
else
f[i][j]=max(f[i-1][j],f[i][j-1]);
}
```
离散化$O(nlogn)$
```cpp
for(fint i=1;i<=n;i++)
cin>>a[i];
for(fint i=1;i<=n;i++)
cin>>b[i];
for(fint i=1;i<=n;i++)
sa[a[i]]=i;
int cnt=0;
for(fint i=1;i<=n;i++)
if(sa[b[i]])
sb[++cnt]=sa[b[i]];
memset(g,0x3f,sizeof(g));
int maxxs=0;
for(fint i=1;i<=cnt;i++)
{
int pos=lower_bound(g+1,g+n+1,sb[i])-g;
maxxs=max(pos,maxxs);
g[pos]=sb[i];
}
cout<<maxxs;
```
#### [6,组合数问题](https://www.luogu.com.cn/problem/P2822)
$f_{i,j}=f_{i-1,j-1}+f_{i-1,j}$
```cpp
signed main()
{
int n,m;
n=read();
m=read();
int t=0;
for(fint i=0;i<=2000;i++)
a[i][0]=1;
a[1][1]=1;
for(fint i=2;i<=2000;i++)
for(fint j=1;j<=i;j++)
a[i][j]=(a[i-1][j-1]+a[i-1][j])%m;
for(fint i=2;i<=2000;i++)
{
for(fint j=1;j<=i;j++)
{
s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1];
if(!a[i][j])
s[i][j]++;
}
s[i][i+1]=s[i][i];
}
int c,b;
for(int i=1;i<=n;i++)
{
t=0;
c=read();
b=read();
if(b>c)
b=c;
cout<<s[c][b]<<endl;
}
return 0;
}
```
#### [7,不等数列](https://www.luogu.com.cn/problem/P2401)
$f_{i,j}=f_{i-1,j-1}*(i-j)+f_{i-1,j}*(j+1)$
```cpp
for(fint i=1;i<=n;i++)
f[i][0]=1,f[i][i-1]=1;
for(fint i=2;i<=n;i++)
for(fint j=1;j<i;j++)
f[i][j]=max(f[i-1][j-1]*(i-j)+f[i-1][j]*(j+1),f[i][j]);
```
#### [8,数楼梯](https://www.luogu.com.cn/problem/P1255)
$f_{i,j}=f_{i-1}+f_{i-2}$
需要高精!!!
#### [9,蜜蜂路线](https://www.luogu.com.cn/problem/P2437)
式子同上,高精省略
```cpp
int main()
{
int m,n;
cin>>m>>n;
f[1]="1",f[2]="1";
for(fint i=3;i<=n-m+1;i++)
f[i]=adds(f[i-1],f[i-2]);
cout<<f[n-m+1];
return 0;
}
```
#### [10,月落乌啼算钱](https://www.luogu.com.cn/problem/P1720)
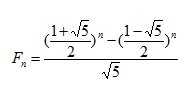
式子仍然同上。然而也可以用以上公式$O(1)$求
这是神奇的斐波那契数列通项公式,我们可以直接求第n项
代码:
```cpp
#include<bits/stdc++.h>
using namespace std;
signed main()
{
int n;
cin>>n;
printf("%.2f",(pow(((1+sqrt(5))/2),n)-pow(((1-sqrt(5))/2),n))/sqrt(5));
return 0;
}
```
#### [11,Red and Blue Balls](https://www.luogu.com.cn/problem/CF399B)
汉诺塔递推
$f_i=f_{i-1}*2+1$
```cpp
for(fint i=1;i<=n;i++)
f[i]=f[i-1]*2+1,cin>>ch,ch=='B'?ans+=(f[i]-f[i-1]):ans+=0;
```
#### [12,滑雪](https://www.luogu.com.cn/problem/P1434)
比较基础的记搜
```cpp
signed main()
{
n=read();
m=read();
for(fint i=1;i<=n;i++)
for(fint j=1;j<=m;j++)
{
h[i][j]=read();
f[i][j]=1;
}
int tot=0;
for(fint i=1;i<=n;i++)
for(fint j=1;j<=m;j++)
tot=max(tot,mfs(i,j));
cout<<tot;
return 0;
}
inline int mfs(int x,int y)
{
int maxxs=0;
if(f[x][y]!=1)
return f[x][y];
if(x>1&&y>=1&&x<=n&&y<=m&&h[x-1][y]>h[x][y])
maxxs=max(maxxs,mfs(x-1,y));
if(x>=1&&y>1&&x<=n&&y<=m&&h[x][y-1]>h[x][y])
maxxs=max(maxxs,mfs(x,y-1));
if(x>=1&&y>=1&&x<n&&y<=m&&h[x+1][y]>h[x][y])
maxxs=max(maxxs,mfs(x+1,y));
if(x>=1&&y>=1&&x<=n&&y<m&&h[x][y+1]>h[x][y])
maxxs=max(maxxs,mfs(x,y+1));
return f[x][y]=maxxs+1;
}
```
#### [13,挖地雷](https://www.luogu.com.cn/problem/P2196)
若i,j相联通
$f_i=max(f_{j}+a_j,f_i)$
```cpp
int main()
{
cin>>n;
for(fint i=1;i<=n;i++)
cin>>a[i];
for(fint i=1;i<=n;i++)
for(fint j=i+1;j<=n;j++)
cin>>f[i][j];
for(fint i=n;i>=1;i--)
for(fint j=1;j<=n;j++)
if(f[i][j]==1)
dp[i]=max(dp[j]+a[j],dp[i]);
for(fint i=1;i<=n;i++)
dp[i]+=a[i];
int s=0;
for(fint i=1;i<=n;i++)
{
if(dp[i]>maxxs)
maxxs=dp[i],s=i;
}
if(n==11)
cout<<s<<" ";
dfs(s,a[s]);
return 0;
}
inline void dfs(int s,int tot)
{
if(tot==maxxs)
{
for(fint i=1;i<=cnt;i++)
cout<<pre[i]<<" ";
cout<<s;
cout<<endl;
cout<<maxxs;
exit(0);
}
for(fint i=s+1;i<=n;i++)
if(f[s][i]==1)
{
pre[++cnt]=s;
dfs(i,tot+a[i]);
cnt=0;
}
return ;
}
```
#### [14,疯狂的采药](https://www.luogu.com.cn/problem/P1616)
完全背包问题;
$f_j=f_{j-w_i}+v_i$
```cpp
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=m;i++)
cin>>w[i]>>v[i];
for(int i=1;i<=m;i++)
for(int j=w[i];j<=n;j++)
f[j]=max(f[j],f[j-w[i]]+v[i]);
cout<<f[n];
return 0;
}
```
#### [15,5倍经验日](https://www.luogu.com.cn/problem/P1802)
背包问题的改进:
$f_j=max(f_j+los_i,f_{j-w[i]}+win[i]),j∈[x,a_i]$
$f_j+=los_i,j∈[0,a_i)$
```cpp
signed main()
{
int n,x;
cin>>n>>x;
for(fint i=1;i<=n;i++)
cin>>los[i]>>win[i]>>a[i];
for(fint i=1;i<=n;i++)
{
for(fint j=x;j>=a[i];j--)
f[j]=max(f[j]+los[i],f[j-a[i]]+win[i]);//胜败取最优
for(fint j=a[i]-1;j>=0;j--)
f[j]+=los[i];//必败态
}
cout<<5*f[x];
return 0;
}
```
#### [16,尼克的任务](https://www.luogu.com.cn/problem/P1280)
倒着存时间
当前无任务:$f_i=f_{i+1}+1$
当前有任务:$f_i=max(f_i,f_{i+sum_i})$
```cpp
int main()
{
int n,k;
n=read(),k=read();
for(fint i=1;i<=k;i++)
a[i].st=read(),a[i].en=read(),cou[a[i].st]++;
sort(a+1,a+k+1,cmp);
int cnt=1;
for(fint i=n;i>0;i--)
if(!cou[i])
f[i]=f[i+1]+1;
else
for(fint j=1;j<=cou[i];j++)
{
if(f[i+a[cnt].en]>f[i])
f[i]=f[i+a[cnt].en];
cnt++;
}
cout<<f[1];
return 0;
}
```
#### [17,摆花](https://www.luogu.com.cn/problem/P1077)
其实很显然三维DP
$f_{i,j}+=f_{i-1,j-k}$
```cpp
signed main()
{
int n,m;
cin>>n>>m;
for(fint i=1;i<=n;i++)
cin>>a[i];
f[0][0]=1;
for(fint i=1;i<=n;i++)
for(fint j=0;j<=m;j++)
for(fint k=0;k<=a[i];k++)
f[i][j]+=f[i-1][j-k],f[i][j]%=mods;
cout<<f[n][m];
return 0;
}
```
#### [18,Redistribution](https://atcoder.jp/contests/abc178/tasks/abc178_d)
跟上一题类似
$f_i+=f_{i-j}$
注意取模;
代码:
```cpp
signed main()
{
int n;
cin>>n;
f[1]=f[2]=0;
for(fint i=3;i<=h;i++)
f[i]=1;
for(fint i=3;i<=h;i++)
for(fint j=3;j<i;j++)
if(i-j>=3)
f[i]+=f[i-j],f[i]%=mods;
cout<<f[n];
return 0;
}
```
#### [19,木棍加工](https://www.luogu.com.cn/problem/P1233)
比较基础的LIS,先根据l排序,再求w的**最小下降子序列个数即最长上升子序列长度**
```cpp
int main()
{
int n;
cin>>n;
for(fint i=1;i<=n;i++)
cin>>a[i].l>>a[i].w;
sort(a+1,a+n+1,cmp);
for(fint i=1;i<=n;i++)
for(fint j=i-1;j>0;j--)
if(a[i].w>a[j].w)
f[i]=max(f[i],f[j]+1);
int maxxs=0;
for(fint i=1;i<=n;i++)
maxxs=max(maxxs,f[i]);
cout<<maxxs+1;
return 0;
}
inline bool cmp(node aa,node bb)
{
if(aa.l==bb.l)
return aa.w>bb.w;
return aa.l>bb.l;
}
```
#### [20,合唱队形](https://www.luogu.com.cn/problem/P1091)
从前到后跑LIS,再从后往前跑LIS,求最值,用n减该值即为所求。
```cpp
int main()
{
int n;
cin>>n;
for(fint i=1;i<=n;i++)
cin>>a[i],f[i]=1,g[i]=1;
for(fint i=2;i<=n;i++)
for(fint j=1;j<i;j++)
if(a[j]<a[i])
f[i]=max(f[i],f[j]+1);
for(fint i=n-1;i>=1;i--)
for(fint j=n;j>i;j--)
if(a[j]<a[i])
g[i]=max(g[i],g[j]+1);
int maxxs=0;
for(fint i=1;i<=n;i++)
maxxs=max(g[i]+f[i],maxxs);
cout<<n-maxxs+1;
return 0;
}
```
#### [21,Golden Sword](https://www.luogu.com.cn/problem/P5858)
设当前锅内容量为j,材料数为i,腾出j-k个材料后放入第i个材料所加耐久即为$f[i-1][k]+a[i]*j$
$f_{i,j}=max(f_{i,j},f_{i,k}+a[i]*j)$
```cpp
signed main()
{
int n,w,s;
cin>>n>>w>>s;
for(fint i=1;i<=n;i++)
cin>>a[i];
for(fint i=0;i<=n;i++)
for(fint j=0;j<=w;j++)
f[i][j]=-inf;
f[0][0]=0;
for(fint i=1;i<=n;i++)//n种材料
for(fint j=w;j>=1;j--)//容纳s个原料
for(fint k=min(w,j+s-1);k>=j-1;k--)//腾出k-j个元素前的材料总数
f[i][j]=max(f[i-1][k]+a[i]*j,f[i][j]);
int maxxs=-inf;
for(fint i=0;i<=w;i++)
maxxs=max(maxxs,f[n][i]);
cout<<maxxs;
return 0;
}
```
#### [22,Permutations](https://www.luogu.com.cn/problem/SP64)
式子:
$f_{i,j}=f_{i,j}+∑_{k=1}^{i-1}f_{i-1,j-k}$
$O(n^3)DP$
#### [23,求逆序对](https://www.luogu.com.cn/problem/P1521)
式子同上
```cpp
int main()
{
ios::sync_with_stdio(false);
f[1][0]=1;
for(fint i=1;i<=15;i++)
for(fint j=0;j<=100;j++)
for(fint k=0;k<=i-1;k++)
f[i][j]+=f[i-1][j-k];
int T;
cin>>T;
while(T--)
{
int n,m;
cin>>n>>m;
cout<<f[n][m]<<endl;
}
return 0;
}
```
#### [24,逆序对数列](https://www.luogu.com.cn/problem/P2513)
大体上和上面两道差不多。但是需要用前缀和优化一下
先加上整个$f_{i-1,j}$再减去$j>=i-1$的部分
$f_{i,j}=f_{i-1,j}-f_{i-1,j-i+1}$
```cpp
for(fint i=1;i<=n;i++)
{
for(fint j=0;j<=k;j++)
{
tot+=f[i-1][j];
f[i][j]+=tot;
if(j>=i-1)
tot-=f[i-1][j-i+1]
}
}
```
#### [25,红牌](https://www.luogu.com.cn/problem/P1130)
普及组难度DP
$f_{i,j}=min(f_{i-1,j},f_{i-1,j-1})+a_{i,j}$
```cpp
int main()
{
int n,m;
cin>>n>>m;
for(fint i=1;i<=m;i++)
for(fint j=1;j<=n;j++)
cin>>a[j][i];
for(fint i=1;i<=n;i++)
for(fint j=1;j<=m;j++)
f[i][j]=min(f[i-1][j],f[i-1][j-1!=0?j-1:m])+a[i][j];
int ans=236582945;
for(fint i=1;i<=m;i++)
ans=min(ans,f[n][i]);
cout<<ans;
return 0;
}
```
#### [26,青蛙过河](https://www.luogu.com.cn/problem/P1244)
这题果然毒瘤,作为一道NOI原题。
1,首先,青蛙只能往前跳,不能往后跳,而且只能12345这样排下去,所以要想使最多的青蛙到达对岸,只需使编号最大的青蛙首先跳到对岸。
2,要想使编号最大的青蛙首先跳到对岸,只需让河面上承载最多的青蛙。而荷叶上只能承载一只青蛙,所以需要让青蛙尽可能多地叠到石墩上
3,$f[i]$表示当有k个荷叶,i个石墩时过河青蛙的最大数量
4,若有k个荷叶,没有石墩,则最多有k+1个青蛙。所以$f[0]=k+1$
5,若有k个荷叶,1个石墩,则只需要使石墩上承载最多的青蛙。进一步分析,我们只需要将石墩当做对岸,这样就变成1的情况了。所以f[1]=f[0]+k+1;同理:若有k个荷叶,2个石墩,则需要先让石墩1作为对岸,叠完后再让石墩2作为对岸。所以f[2]=f[1]+f[0]+k+1;
$f_i=(∑_{j=0}^{i-1}f_j)+k+1$
```cpp
int main()
{
int h,k;
cin>>h>>k;
f[0]=k+1;
int now=f[0]+k+1;
for(fint i=1;i<=h;i++)
f[i]=now,now+=f[i];
cout<<f[h];
return 0;
}
```
#### [27,NASA的食物计划](https://www.luogu.com.cn/problem/P1507)
二维费用背包问题
$f_{j,k}=max(f_{j,k},f_{j-v_i,k-m_i}+t_i)$
```cpp
int main()
{
int v_max,m_max;
cin>>v_max>>m_max;
int n;
cin>>n;
for(fint i=1;i<=n;i++)
cin>>v[i]>>m[i]>>t[i];
for(fint i=1;i<=n;i++)
for(fint j=v_max;j>=v[i];j--)
for(fint k=m_max;k>=m[i];k--)
f[j][k]=max(f[j][k],f[j-v[i]][k-m[i]]+t[i]);
cout<<f[v_max][m_max];
return 0;
}
```
#### [28,Generic Cow Protests](https://www.luogu.com.cn/problem/P1569)
前缀和处理一下,当一个区间$(i,j)$的理智和大于0,就更新
$f_{i}=max(f_i,f_j+1)$
```cpp
int main()
{
ios::sync_with_stdio(false);
int n;
cin>>n;
for(fint i=1;i<=n;i++)
cin>>a[i],s[i]=s[i-1]+a[i],a[i]>=0?f[i]=1:f[i]=-1e8;
for(fint i=1;i<=n;i++)
for(fint j=1;j<i;j++)
if(s[i]-s[j]>=0)
f[i]=max(f[i],f[j]+1);
return f[n]==-1e8?cout<<"Impossible":cout<<f[n],0;
}
```
#### [29,神奇的四次方数](https://www.luogu.com.cn/problem/P1679)
先预处理出$i^4$数,然后以该数为容量,1为价值跑完全背包即可。
$f_j=min(f_{j-w_i}+v_i,f_j)$
```cpp
int main()
{
int m;
cin>>m;
for(fint i=1;i<=18;i++)
w[i]=i*i*i*i;
memset(f,0x3f,sizeof(f));
f[0]=0;
for(fint i=1;i<=18;i++)
for(fint j=w[i];j<=m;j++)
f[j]=min(f[j-w[i]]+1,f[j]);
cout<<f[m];
return 0;
}
```
#### [31,回文字串](https://www.luogu.com.cn/problem/P1435)
求出最长公共回文序列,然后n-该序列长度即为答案。
正序与倒序“公共”的部分就是我们回文的部分,如果把正序与倒序公共的部分减去你就会惊奇的发现剩余的字符就是你所要添加的字符
$f_{i,j}=max(f_{i-1,j-1}+1,f_{i,j})||f_{i,j}=max(f_{i,j-1},f_{i-1,j})$
普通版:
```cpp
int main()
{
scanf("%s",a+1);
int len=strlen(a+1);
for(fint i=1;i<=len;i++)
b[i]=a[len-i+1];
for(fint i=1;i<=len;i++)
for(fint j=1;j<=len;j++)
if(a[i]==b[j])
f[i][j]=max(f[i][j],f[i-1][j-1])+1;
else
f[i][j]=max(f[i-1][j],f[i][j-1]);
cout<<len-f[len][len];
return 0;
}
```
优化后版本见DP优化篇
#### [32,书本整理](https://www.luogu.com.cn/problem/P1103)
说实话,这道黄题我是看了很久都无从下手。最后还是在题解的帮助下AC了。这道题的状态确实不好想,开始我觉得状态$f_{i,j}$会从$f_{i-1,j-k}$处转移,不过事实上没那么简单。
我们用三层循环$i,j,l$表示第i本书与第j本相邻,序列长度为l
状态$f_{i,j}$便从上一本与他相邻的位置$j$转移,此时序列长度为$l-1$
所以得到式子:
$f_{i,l}=min(f_{i,l},f_{j,l-1}+△h)$
代码:
```cpp
int main()
{
int n,m;
cin>>n>>m;
m=n-m;
for(fint i=1;i<=n;i++)
cin>>a[i].c>>a[i].k;
sort(a+1,a+n+1,cmp);
memset(f,0x3f,sizeof(f));
for(fint i=1;i<=n;i++)
f[i][1]=0;
for(fint i=2;i<=n;i++)//第i本
for(fint j=1;j<i;j++)//与j相邻
for(fint l=2;l<=min(i,m);l++)
f[i][l]=min(f[i][l],f[j][l-1]+abs(a[i].k-a[j].k));
int ans=54674895;
for(fint i=m;i<=n;i++)
ans=min(ans,f[i][m]);
cout<<ans;
return 0;
}
```
#### [33,数的拆分](http://acm.xidian.edu.cn/problem.php?id=1096)
把N拆成若干个**无序**的正整数的和的方案数(5 = 1 + 2 + 2 = 2 + 1 + 2算一种方案)
我们设$f_{i,j}$为和为$i$且单个数不超过$j$的拆分方案.这时候,我们有两种方式可以得到递推式:
1,求删去$j$后$f_{i-j,j}$的方案数。
2,不超过$j-1$且和为$i$的方案数。
先来看1,我们单个数最大为j,也就是说$f_{i,j}$可以从此前删去j的状态继承
再来看2,$≤j-1$的数一定$≤j$,所以$f_{i,j}$一定可以从$f_{i,j-1}$继承.
所以:
$f_{i,j}=f_{i,j-1}+f_{i-j,j}$
By the way,如果整数互不相同,那么:
$f_{i,j}=f_{i-j,j-1}+f_{i-j,j}$
偷个懒,代码不写了QAQ。
#### [34,通天之潜水](https://www.luogu.com.cn/problem/P1759)
第一问:二维费用背包问题
$f_{j,k}=max(f_{j,k},f_{j-v_i,k-m_i}+t_i)$
```cpp
int main()
{
int m,v,n;
cin>>m>>v>>n;
for(fint i=1;i<=n;i++)
cin>>w[i]>>zu[i]>>t[i];
for(fint i=1;i<=n;i++)
for(fint j=m;j>=w[i];j--)
for(fint k=v;k>=zu[i];k--)
f[j][k]=max(f[j][k],f[j-w[i]][k-zu[i]]+t[i]);
cout<<f[m][v]<<endl;
return 0;
}
```
第二问,输出路径
记录一下背包在哪更新,然后dfs即可。
非常不错的DP+DFS
最终代码:
```cpp
int main()
{
int m,v,n;
cin>>m>>v>>n;
for(fint i=1;i<=n;i++)
cin>>w[i]>>zu[i]>>t[i];
for(fint i=1;i<=n;i++)
for(fint j=m;j>=w[i];j--)
for(fint k=v;k>=zu[i];k--)
if(f[j-w[i]][k-zu[i]]+t[i]>f[j][k])
f[j][k]=f[j-w[i]][k-zu[i]]+t[i],vis[i][j][k]=1;
cout<<f[m][v]<<endl;
dfs(n,m,v);
return 0;
}
inline void dfs(int n,int m,int v)
{
if(vis[n][m][v])
{
if(n==1)
cout<<1<<" ";
else
m-w[n]>=0&&v-zu[n]>=0?dfs(n-1,m-w[n],v-zu[n]):dfs(n-1,m,v),cout<<n<<" ";
return ;
}
if(n==1)
return ;
if(!vis[n][m][v])
dfs(n-1,m,v);
return ;
}
```
#### [35,迷之阶梯](https://www.luogu.com.cn/problem/P1929)
对于第一条规则:
$if(a_i=a_{i-1}+1)f_i=min(f_{i-1}+1,f_i)$
对于二三条规则。设当前在j,往后退到k,跳$2^{j-k+1}$格后能到达i
$f_i=min(f_i,f_j+(j-k+1))$
```cpp
int main()
{
int n;
cin>>n;
for(fint i=1;i<=n;i++)
cin>>a[i];
memset(f,0x3f,sizeof(f));
f[1]=0;
for(fint i=2;i<=n;i++)
{
if(a[i-1]+1==a[i])
f[i]=min(f[i-1]+1,f[i]);
for(fint j=i-1;j>=1;j--)
for(fint k=j-1;k>=1;k--)
if(a[k]+(1<<(j-k))>=a[i])
f[i]=min(f[i],f[j]+(j-k+1));
}
f[n]!=1061109567?cout<<f[n]:cout<<-1;
return 0;
}
```
#### [36,龙兄摘苹果](https://www.luogu.com.cn/problem/P2028)
第二类斯特林数递推:
$f_{i,j}=f_{i-1,j-1}+f_{i-1,j}×j$
```cpp
signed main()
{
int n,k,p;
cin>>n>>k>>p;
for(fint i=1;i<=n;i++)
f[i][1]=1;
for(fint i=1;i<=n;i++)
for(fint j=2;j<=k;j++)
f[i][j]=(f[i-1][j-1]%p+(f[i-1][j]%p*j%p)%p%p)%p,f[i][j]%=p;
cout<<f[n][k]%p;
return 0;
}
```
#### [37,Shaass and Bookshelf](https://www.luogu.com.cn/problem/CF294B)
背包加贪心
$f_j=min(f_{j-v[i]}+w_i,f_j)$
```cpp
int main()
{
int n;
cin>>n;
int tot=0;
for(fint i=1;i<=n;i++)
cin>>v[i]>>w[i],tot+=v[i];
memset(f,0x3f,sizeof(f));
f[0]=0;
int ans=0;
for(fint i=1;i<=n;i++)
{
for(fint j=tot;j>=v[i];j--)
f[j]=min(f[j],f[j-v[i]]+w[i]);
for(fint j=tot;j>=0;j--)
if(tot-j>=f[j])
{
ans=tot-j;
break;
}
}
cout<<ans;
return 0;
}
```
#### [38,Partitioning by Palindromes](https://www.luogu.com.cn/problem/UVA11584)
首先要熟悉回文串的性质:
1,对于小于等于两位的回文串,首项=末项。
2,对于大于两位的回文串,首项=末项且除了首项和末项之外成回文。
我们可以用$f_{i,j}$记录从i到j的回文情况。
然后进行DP
$dp_i=min(dp_i,dp_{j-1}+1)$这其实和$O(n^2)$的LIS问题比较像
代码:
```cpp
while(T--)
{
string a;
cin>>a;
int len=a.size();
memset(dp,0x3f,sizeof(dp));
memset(f,0,sizeof(f));
for(fint i=0;i<len;i++)
for(fint j=0;j<=i;j++)
if(a[i]==a[j]&&(i-j+1<=2||f[i-1][j+1]))
{
f[i][j]=1;
i!=0?dp[i]=min(dp[i],dp[j-1]+1):dp[i]=1;
}
cout<<dp[len-1]<<endl;
}
```
#### [39,开心的金明](https://www.luogu.com.cn/problem/P1060)
算是比较裸的01背包,注意价值是价格*重要度
$f_j=max(f_j,f_{j-pri_i}+pri_i*lev_i)$
```cpp
int main()
{
int n,m;
cin>>n>>m;
for(fint i=1;i<=m;i++)
cin>>pri[i]>>lev[i];
for(fint i=1;i<=m;i++)
for(fint j=n;j>=pri[i];j--)
f[j]=max(f[j],f[j-pri[i]]+pri[i]*lev[i]);
cout<<f[n];
return 0;
}
```
#### [40,方格取数](https://www.luogu.com.cn/problem/P1004)
同时处理两条不相交的路径,有四种情况
下下,下右,右下,右右,得到状态转移方程
$f[i][j][k][l]=max(max(f[i-1][j][k-1][l],f[i-1][j][k][l-1]),max(f[i][j-1][k-1][l],f[i][j-1][k][l-1]))+a[i][j]+a[k][l];$
代码:
```cpp
int main()
{
int n;
cin>>n;
int x,y,z;
while(1)
{
cin>>x>>y>>z;
if(x==0&&y==0&&z==0)
break;
a[x][y]=z;
}
for(fint i=1;i<=n;i++)
for(fint j=1;j<=n;j++)
for(fint k=1;k<=n;k++)
for(fint l=1;l<=n;l++)
{
f[i][j][k][l]=max(max(f[i-1][j][k-1][l],f[i-1][j][k][l-1]),max(f[i][j-1][k-1][l],f[i][j-1][k][l-1]))+a[i][j]+a[k][l];
if(i==k&&j==l)
f[i][j][k][l]-=a[i][j];
}
cout<<f[n][n][n][n];
return 0;
}
```
#### [41,Leaping Tak](https://atcoder.jp/contests/abc179/tasks/abc179_d)
CF的题,很容易想到:
$\large f_i=∑_{j=l}^{r-1}f_{i-j}$
但是复杂度显然太高,所以考虑维护一发前缀和,
即$\large s_i=s_{i-1}+f_i$,这样复杂度从$O(n^2)$(最坏)成功降至
$O(nk)$(严格),这样便可AC此题
代码:
```cpp
signed main()
{
int n,k;
cin>>n>>k;
for(fint i=1;i<=k;i++)
cin>>l[i]>>r[i];
f[1]=1,s[1]=1;
for(fint i=2;i<=n;i++)
{
for(fint j=1;j<=k;j++)
f[i]=f[i]-(s[(i-r[j]-1<0?0:i-r[j]-1)]-s[i-l[j]<0?0:i-l[j]]),f[i]%=mods;
s[i]=s[i-1]+f[i],s[i]%=mods;
}
cout<<(f[n]+mods)%mods;
return 0;
}
```
#### [42,樱花](https://www.luogu.com.cn/problem/P1833)
简单的混合背包,然而会T,先上优化前代码:
可以考虑二进制拆分优化复杂度,在DP优化部分有出现哦!
```cpp
int main()
{
// freopen("B.in","r",stdin);
// freopen("B.out","w",stdout);
int ha,ma,hb,mb,n;
scanf("%d:%d%d:%d%d",&ha,&ma,&hb,&mb,&n);
int tim=(hb-ha)*60+(mb-ma);
//cout<<t;
for(fint i=1;i<=n;i++)
cin>>t[i]>>c[i]>>p[i];
for(fint i=1;i<=n;i++)
{
if(p[i]==0)
for(fint j=t[i];j<=tim;j++)
f[j]=max(f[j],f[j-t[i]]+c[i]);
else
for(fint j=1;j<=p[i];j++)
for(fint k=tim;k>=t[i];k--)
f[k]=max(f[k],f[k-t[i]]+c[i]);
}
cout<<f[tim];
return 0;
}
```
#### [43,字串距离](https://www.luogu.com.cn/problem/P1279)
DP,有点像LCS问题。
如果上一位有空格$f_{i,j}=min(f_{i-1,j}+k,f_{i,j-1}+k)$
如果上一位没空格$f_{i,j}=f_{i-1,j-1}+abs(a_i-b_j)$
代码:
```cpp
int main()
{
scanf("%s",a+1);
scanf("%s",b+1);
int lena=strlen(a+1),lenb=strlen(b+1);
int k;
cin>>k;
for(fint i=1;i<=lena;i++)
f[i][0]=i*k;
for(fint i=1;i<=lenb;i++)
f[0][i]=i*k;
for(fint i=1;i<=lena;i++)
for(fint j=1;j<=lenb;j++)
f[i][j]=min(min(f[i-1][j]+k,f[i][j-1]+k),f[i-1][j-1]+abs(a[i]-b[j]));
cout<<f[lena][lenb];
return 0;
}
```
#### [44,小A点菜](https://www.luogu.com.cn/problem/P1164)
也是一个相当经典的模型,类似与背包或者拆分数。
$f_{i}+=f_{i-v_i}$
代码:
```cpp
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
cin>>v[i];
sort(v+1,v+1+n);
for(int i=1;i<=n;i++)
for(int j=m;j>=v[i];j--)
f[j]+=f[j-v[i]];
cout<<f[m];
return 0;
}
```
#### [45,选举 Easy](https://www.luogu.com.cn/problem/P4394)
01背包问题,先统计总和,然后对满足超过一半的情况跑个背包即可。
```cpp
int main()
{
int n;
cin>>n;
int sum=0;
for(fint i=1;i<=n;i++)
cin>>a[i],sum+=a[i];
sum>>=1;
int ans=0;
sort(a+1,a+n+1);
for(fint i=1;i<=n;i++)
for(fint j=(sum<<1);j>=sum;j--)
{
f[j]=max(f[j-a[i]]+a[i],f[j]);
if(f[j]>=sum&&f[j]>ans)
ans=f[j];
}
cout<<ans;
return 0;
}
```
#### [46,排兵布阵](https://www.luogu.com.cn/problem/P5322)
分组背包,贪心。将用兵数从小到大排序,然后进行1-s的分组背包即可
$\large f_j=max(f_j,f_{j-2*a_{i,k}}+i*k)$
```
int main()
{
int s,n,m;
cin>>s>>n>>m;
for(fint i=1;i<=s;i++)
for(fint j=1;j<=n;j++)
cin>>a[j][i];
for(fint i=1;i<=n;i++)
{
sort(a[i]+1,a[i]+s+1);
for(fint j=m;j>0;j--)
for(fint k=1;k<=s;k++)
if(j>2*a[i][k])
f[j]=max(f[j-2*a[i][k]-1]+i*k,f[j]);
}
cout<<f[m];
return 0;
}
```
#### [47,传纸条](https://www.luogu.com.cn/problem/P1006)
和方格取数几乎一毛一样QAQ
```cpp
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
cin>>s[i][j];
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
for(int k=1;k<=n;k++)
for(int l=1;l<=m;l++)
{
t[i][j][k][l]+=max(max(t[i-1][j][k-1][l],t[i-1][j][k][l-1]),max(t[i][j-1][k-1][l],t[i][j-1][k][l-1]))+s[i][j]+s[k][l];
if(i==k&&j==l)
t[i][j][k][l]-=s[i][j];
}
cout<<t[n][m][n][m];
return 0;
}
```
#### [48,通天之分组背包](https://www.luogu.com.cn/problem/P1757)
说实话,分组背包的题目并不多,这竟是本蒟蒻的第一篇分组背包的题目。
在输入时用$num_i$记录第i组人数,用$a[i][num[i]]$记录第i组第$num_i$个成员的物品序号。
$f_j=max(f_{j-w[a[i][k]]}+v[a[i][k]],f_j)$
代码:
```cpp
int main()
{
int m,n;
cin>>m>>n;
int grop,grop_tot;
for(fint i=1;i<=n;i++)
{
cin>>w[i]>>v[i]>>grop;
num[grop]++;
a[grop][num[grop]]=i;
grop_tot=max(grop_tot,grop);
}
for(fint i=1;i<=grop_tot;i++)//枚举组
for(fint j=m;j>0;j--)//枚举容量
for(fint k=1;k<=num[i];k++)//枚举组内成员
if(j>=w[a[i][k]])
f[j]=max(f[j],f[j-w[a[i][k]]]+v[a[i][k]]);
cout<<f[m];
return 0;
}
```
#### [49,ZBRKA](https://www.luogu.com.cn/problem/P6323)
逆序对数量问题是一个相当经典的DP问题。当我们计算到第$i$位时其实只需要考虑将$i$插入到$i-1$个位置即可。插入到第$k$个位置就会产生新的$k$个逆序对,所以得到转移方程:
$f_{i,j}+=∑_{k=1}^{i-1}f_{i-1,j-k}$
代码:
```cpp
f[1][0]=1;
for(fint i=1;i<=n;i++)
for(fint j=0;j<=c;j++)
{
for(fint k=0;j-k>=0&&k<=i-1;k++)
{
if(j-k>=0)
f[i][j]+=f[i-1][j-k],f[i][j]%=mods;
}
cout<<f[i][j]<<" ";
}
```
时间复杂度$O(nc^2)$,得分56分。
考虑优化,直觉告诉我们可以用前缀和思维压掉一维。
我们先累加上所有之前的$f_{i-1,j}$,然后再减去超出范围de部分,剩下的部分,就是满足条件的种类数量了QAQ。
代码:
```cpp
signed main()
{
int n,c;
cin>>n>>c;
f[1][0]=1;
for(fint i=1;i<=n;i++)
{
long long tot=0;
for(fint j=0;j<=c;j++)
{
tot=(tot%mods+f[i-1][j]%mods)%mods;
f[i][j]=(f[i][j]%mods+tot%mods)%mods;
if(j>=i-1)
tot=(tot%mods-f[i-1][j-i+1]%mods)%mods;
}
}
cout<<(f[n][c]+mods)%mods;
return 0;
}
```
#### [50,过河卒](https://www.luogu.com.cn/problem/P1002)
首先预处理马可以爬到的位置,然后对于每个未被覆盖过的位置,满足:$a_{i,j}=a_{i-1,j}+a_{i,j-1}$
```cpp
int main()
{
int xa,xb,ya,yb;
cin>>xa>>ya>>xb>>yb;
xa++;ya++;xb++;yb++;
for(int i=1;i<=xa;i++)
for(int j=1;j<=ya;j++)
a[i][j]=1;
a[xb][yb]=0;
if(xb-2>=0&&yb-1>=0)
a[xb-2][yb-1]=0;
if(xb-2>=0&&yb+1<=ya)
a[xb-2][yb+1]=0;
if(xb+2<=xa&&yb+1<=ya)
a[xb+2][yb+1]=0;
if(xb+2<=xa&&yb-1>=0)
a[xb+2][yb-1]=0;
if(xb-1>=0&&yb+2<=ya)
a[xb-1][yb+2]=0;
if(xb+1<=xa&&yb+2<=ya)
a[xb+1][yb+2]=0;
if(xb-1>=0&&yb-2>=0)
a[xb-1][yb-2]=0;
if(xb+1<=xa&&yb-2>=0)
a[xb+1][yb-2]=0;
a[0][1]=1;
for(int i=1;i<=xa;i++)
for(int j=1;j<=ya;j++)
{
if(a[i][j]==0)
continue;
else
a[i][j]=a[i-1][j]+a[i][j-1];
}
cout<<a[xa][ya];
return 0;
}
```
#### [51,Pokémon Army](https://www.luogu.com.cn/problem/CF1420C1)
$f_i$是这一步做加法的最大值,$g_i$是这一步做减法的最大值,初始f数组与g数组均为-0x3f
我是从2开始DP的,由于$f_i$在2这一步做加法,且第一步不能做减法,所以直接跳过第一步,又$f_i$是从$\large g_{i-1}$转移过来的,所以$g_1=0$。同理,$g_i$要在第二步做减法,那第一步必是加法。所以$\large f_1=a_1$
我们需要维护两个状态:初始化状态和更新状态
初始化状态就是每次我们把$f_i$设为$f_{1}$到$f_{i-1}$的最大值,$g_i$设为$g_{1}$到$g_{i-1}$的最大值。然后再考虑转移:
```cpp
f[i]=max(g[i-1]+a[i],f[i]),g[i]=max(f[i-1]-a[i],g[i]);
```
看能否把从g过来这步做加法和从f过来这步做减法给更新掉。然后更新此时f与g的最大值便于下一步使用。
最后,上代码:
```cpp
signed main()
{
ios::sync_with_stdio(false);
int T;
cin>>T;
while(T--)
{
memset(f,-0x3f,sizeof(f));
memset(g,-0x3f,sizeof(g));
int n,q;
cin>>n>>q;
for(fint i=1;i<=n;i++)
cin>>a[i];
f[1]=a[1],g[1]=0;
int max_f=a[1],max_g=0;
for(fint i=2;i<=n;i++)
{
f[i]=max(max_f,f[i]),g[i]=max(max_g,g[i]);
f[i]=max(g[i-1]+a[i],f[i]),g[i]=max(f[i-1]-a[i],g[i]);
max_f=f[i],max_g=g[i];
}
int ans=-inf;
for(fint i=1;i<=n;i++)
ans=max(ans,max(f[i],g[i]));
cout<<ans<<endl;
}
return 0;
}
```
#### [52,Trains and Statistic](https://www.luogu.com.cn/problem/CF675E)
其实这道题就是一道DP+数据结构维护区间最值,我们很自然的可以想到用线段树来维护QAQ。
已知从$i$最多能跑到 $[i+1,a[i]]$,我们一定要从 $[i+1,a[i]]$中间一个点转移过去的。很显然,我们应该贪心地从该区间中间选取一个点M,使得 $a[M]$最大。这样才能找到最小车票花费。
如何进行状态转移呢?我们先从$i$走到$k$,此时的花费$f_M + n-M$,但是 $[M+1,a[i]]$这部分被重复计算了,我们要减去TA。在加上第一步
得到方程:$f_i=f_M+(n-1)-(a_i-M)$
PS:M部分即为我们需要维护的区间最值
很显然,我们需要使用线段树来维护区间最大值。但这个区间最值又有些不一样。因为我们要求的是$a[m]$能到的最大车站,而不是$a[m]$的最大值。所以,我们在建树的时候需要同时记录车站与能到的车站两个变量,这种操作或许可以被称作**双权值线段树**(我自己编的。。。)当然喽,查询的时候也要在能到的车站最大时返回当前车站。
好像有点小麻烦,但实际上只要理解了线段树操作的本质,就还是很容易打出来的。
```cpp
#include<bits/stdc++.h>
#define fint register int
#define h 5001
#define p 4570944
#define ls x<<1
#define rs x<<1|1
#define tt t[x].tot
#define ll t[x].l
#define rr t[x].r
#define int long long
using namespace std;
struct node
{
int l;
int r;
int tot;
int tag;
}
t[p];
int maxxs,max_id;
int a[p],f[p],num[p];
inline int query(int x,int l,int r);
inline void build(int x,int l,int r);
signed main()
{
int n;
cin>>n;
for(fint i=1;i<n;i++)
cin>>a[i];
a[n]=n;
for(fint i=1;i<=n;i++)
num[i]=i;
build(1,1,n);
int ans=0;
for(fint i=n-1;i>=1;i--)
{
maxxs=-1,max_id=0;
int M=query(1,i+1,a[i]);
// cout<<i+1<<" "<<a[i]<<endl;
// cout<<M<<" "<<endl;
f[i]=f[M]+(n-i)-(a[i]-M);
ans+=f[i];
}
cout<<ans;
return 0;
}
inline void build(int x,int l,int r)
{
ll=l,rr=r;
if(l==r)
{
tt=a[l];
t[x].tag=l;
return ;
}
int mid=(rr+ll)>>1;
build(ls,l,mid);
build(rs,mid+1,r);
if(t[ls].tot>t[rs].tot)
t[x].tag=t[ls].tag;
else
t[x].tag=t[rs].tag;
tt=max(t[ls].tot,t[rs].tot);
return ;
}
inline int query(int x,int l,int r)
{
if(ll>=l&&rr<=r)
{
if(maxxs<tt)
maxxs=tt,max_id=t[x].tag;
return max_id;
}
int mid=(ll+rr)>>1;
int a=0,b=0;
if(l<=mid)
a=query(ls,l,r);
if(r>mid)
b=query(rs,l,r);
return max_id;
}
```
#### [53,玉蟾宫](https://www.luogu.com.cn/problem/P4147)
最大子矩阵问题。可以使用悬线法求解QAQ
推荐一篇blog:[DP专题:悬线法](https://www.cnblogs.com/zhenglw/p/10102833.html)
代码:
```cpp
signed main()
{
int n,m;
cin>>n>>m;
int maxxs=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
cin>>b[i][j];
if(b[i][j]=='F')
a[i][j]=1;
else
a[i][j]=0;
ri[i][j]=j;
le[i][j]=j;
up[i][j]=1;
}
for(int i=1;i<=n;i++)
for(int j=2;j<=m;j++)
if(a[i][j]==1&&a[i][j-1]==1)
le[i][j]=le[i][j-1];
for(int i=1;i<=n;i++)
for(int j=m-1;j>=1;j--)
if(a[i][j]==1&&a[i][j+1]==1)
ri[i][j]=ri[i][j+1];
int j;
for(int i=1;i<=n;i++)
{
for(j=1;j<=m;j++)
{
if(i>1&&a[i-1][j]==1&&a[i][j]==1)
{
le[i][j]=max(le[i][j],le[i-1][j]);
ri[i][j]=min(ri[i][j],ri[i-1][j]);
up[i][j]=up[i-1][j]+1;
}
if((ri[i][j]-le[i][j]+1)*up[i][j]>maxxs)
maxxs=(ri[i][j]-le[i][j]+1)*up[i][j];
}
}
```
#### [54,最大正方形](https://www.luogu.com.cn/problem/P1387)
一道比较基础的二维DP.
如果该位置为1,就从可转移的几个位置的最小值+1转移过来。
$f_{i,j}=min(f_{i-1,j},f_{i,j-1},f_{i-1,j-1})+1$
```cpp
#include<bits/stdc++.h>
#define fint register int
#define h 5001
#define p 448736
using namespace std;
inline int read();
int a[h][h];
int f[h][h];
signed main()
{
int n,m;
n=read(),m=read();
for(fint i=1;i<=n;i++)
for(fint j=1;j<=m;j++)
a[i][j]=read();
int ans=0;
for(fint i=1;i<=n;i++)
for(fint j=1;j<=m;j++)
{
if(a[i][j])
f[i][j]=min(min(f[i-1][j],f[i][j-1]),f[i-1][j-1])+1;
ans=max(ans,f[i][j]);
}
cout<<ans;
return 0;
}
inline int read()
{
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-')
f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*f;
```
基础的悬线法DP求最大子矩阵。用ri,le,up记录向右左上能拓展到的最大距离。
然后更新即可
代码:
```cpp
int main()
{
int n,m;
cin>>n>>m;
for(fint i=1;i<=n;i++)
for(fint j=1;j<=m;j++)
cin>>a[i][j];
for(fint i=1;i<=n;i++)//初始化
for(fint j=1;j<=m;j++)
ri[i][j]=le[i][j]=j,up[i][j]=1;
for(fint i=1;i<=n;i++)
for(fint j=2;j<=m;j++)
if(a[i][j-1]==a[i][j]&&a[i][j]==1)
le[i][j]=le[i][j-1];
for(fint i=1;i<=n;i++)
for(fint j=m-1;j>=1;j--)
if(a[i][j+1]==a[i][j]&&a[i][j]==1)
ri[i][j]=ri[i][j+1];
int ans=0;
for(fint i=1;i<=n;i++)
for(fint j=1;j<=m;j++)
{
if(i>1)
{
if(a[i-1][j]==a[i][j]&&a[i][j]==1)
{
le[i][j]=max(le[i][j],le[i-1][j]);
ri[i][j]=min(ri[i][j],ri[i-1][j]);
up[i][j]=up[i-1][j]+1;
}
}
int a=ri[i][j]-le[i][j]+1;
int b=min(a,up[i][j]);
ans=max(ans,b);
}
cout<<ans;
return 0;
}
```
#### [55,金明的预算方案](https://www.luogu.com.cn/problem/P1064)
**非常非常重要也是有难度**的一道背包DP。
我们先预处理出每件主件的附属(最多俩),然后分类讨论:
只选主,选主副1,选主副2,选主副1副2.
分别列出方程转移即可。
注意我们枚举物品时只对主件进行讨论,如果遇到附件就直接跳过
代码:
```cpp
int main()
{
int n,m;
cin>>n>>m;
int siz;
for(fint i=1;i<=m;i++)
{
cin>>jia[i]>>zhong[i]>>siz;
v[i]=jia[i]*zhong[i];
if(siz==0)
hos[i]=1;
else
if(!vis[siz])
zhu[siz].a=i,vis[siz]=1;
else
zhu[siz].b=i;
}
for(fint i=1;i<=m;i++)
for(fint j=n;j>=0;j--)
{
if(!hos[i])
continue;
if(j>=jia[i])
f[j]=max(f[j],f[j-jia[i]]+v[i]);//只选主件或者不选
if(j>=jia[i]+jia[zhu[i].a])
f[j]=max(f[j],f[j-jia[i]-jia[zhu[i].a]]+v[i]+v[zhu[i].a]);//选主和附1
if(j>=jia[i]+jia[zhu[i].b])
f[j]=max(f[j],f[j-jia[i]-jia[zhu[i].b]]+v[i]+v[zhu[i].b]);//选主和附1
if(j>=jia[i]+jia[zhu[i].a]+jia[zhu[i].b])
f[j]=max(f[j],f[j-jia[i]-jia[zhu[i].a]-jia[zhu[i].b]]+v[i]+v[zhu[i].a]+v[zhu[i].b]);//选主,附1,附2
}
cout<<f[n];
return 0;
}
```
#### [56,棋盘制作](https://www.luogu.com.cn/problem/P1169)
依然悬线法DP
```cpp
signed main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
cin>>a[i][j];
r[i][j]=j;
l[i][j]=j;
up[i][j]=1;
}
for(int i=1;i<=n;i++)
for(int j=2;j<=m;j++)
if(a[i][j]!=a[i][j-1])
l[i][j]=l[i][j-1];
for(int i=1;i<=n;i++)
for(int j=m-1;j>=1;j--)
if(a[i][j]!=a[i][j+1])
r[i][j]=r[i][j+1];
int t=0;
int s=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
if(i>1&&a[i][j]!=a[i-1][j])
{
l[i][j]=max(l[i-1][j],l[i][j]);
r[i][j]=min(r[i-1][j],r[i][j]);
up[i][j]=up[i-1][j]+1;
}
int a=r[i][j]-l[i][j]+1;
int b=min(a,up[i][j]);
t=max(b*b,t);
s=max(a*up[i][j],s);
}
cout<<t;
cout<<endl;
cout<<s;
return 0;
}
```
#### [57,Big Barn](https://www.luogu.com.cn/problem/P2701)
悬线法同上
```cpp
signed main()
{
int n,m;
cin>>n>>m;
int c,d;
for(int k=1;k<=m;k++)
{
cin>>c>>d;
a[c][d]=1;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
r[i][j]=j;
l[i][j]=j;
up[i][j]=1;
}
for(int i=1;i<=n;i++)
for(int j=2;j<=n;j++)
if(a[i][j]==0&&a[i][j-1]==0)
l[i][j]=l[i][j-1];
for(int i=1;i<=n;i++)
for(int j=n-1;j>=1;j--)
if(a[i][j]==0&&a[i][j+1]==0)
r[i][j]=r[i][j+1];
int t=0;
int s=0;
int ts=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
if(i>1&&a[i][j]==0&&a[i-1][j]==0)
{
l[i][j]=max(l[i-1][j],l[i][j]);
r[i][j]=min(r[i-1][j],r[i][j]);
up[i][j]=up[i-1][j]+1;
}
t=r[i][j]-l[i][j]+1;
s=min(t,up[i][j]);
ts=max(ts,s);
}
cout<<ts;
return 0;
}
```
#### [58,激光炸弹](https://www.luogu.com.cn/problem/P2280)
范围hen小,考虑直接枚举。首先二维前缀和求一下,然后找$i+r,j+r$范围内价值最大值即可
$f_{i,j}=f_{i-1,j}+f_{i,j-1}-f_{i-1,j-1}+a_{i,j}$
然后求出所有边长为r得到正方形内的最大价值
$ans=max(ans,f[i+r][j+r]-f[i+r][j]-f[i][j+r]+f[i][j]);$
代码:
```cpp
signed main()
{
int n,r;
cin>>n>>r;
int xi,yi,vi;
for(fint i=1;i<=n;i++)
{
cin>>xi>>yi>>vi;
f[xi+1][yi+1]=vi;
}
int maxxs=0;
for(int i=1;i<=5001;i++)
for(int j=1;j<=5001;j++)
f[i][j]+=f[i-1][j]+f[i][j-1]-f[i-1][j-1];
for(fint i=0;i<=5000-r;i++)
for(fint j=0;j<=5000-r;j++)
maxxs=max(maxxs,f[i][j]-f[i+r][j]-f[i][j+r]+f[i+r][j+r]);
cout<<maxxs;
return 0;
}
```
#### [59,组合数问题](https://www.luogu.com.cn/problem/P2822)
直接怼公式,然后枚举:
```cpp
#include<bits/stdc++.h>
using namespace std;
long long s=1;
long long zu(long long x);
long long pd(long long y,long long z);
int main()
{
int n,m;
cin>>n>>m;
int t=0;
int a,b;
for(int i=1;i<=n;i++)
{
t=0;
cin>>a>>b;
for(int j=1;j<=a;j++)
for(int k=1;k<=min(b,j);k++)
if((pd(j,k))%m==0)
t++;
cout<<t<<endl;
}
return 0;
}
long long zu(long long x)
{
if(x==0)
return 1;
s=1;
for(int i=1;i<=x;i++)
s*=i;
return s;
}
long long pd(long long y,long long z)
{
return zu(y)/(zu(z)*zu(y-z));
}
```
该做法得分:40
考虑优化,组合数可以用杨辉三角推出来。$C_0^0=C_0^i=C_i^i=1$
然后$f_{i,j}=f_{i-1,j-1}+f_{i-1,j}$.枚举即可
代码:
```cpp
int main()
{
int T,k;
cin>>T>>k;
for(fint i=0;i<=2001;i++)
f[i][i]=1,f[i][0]=1;
for(fint i=1;i<=2001;i++)
for(fint j=1;j<i;j++)
f[i][j]=f[i-1][j-1]+f[i-1][j];
// for(fint i=0;i<=10;i++)
// {
// for(fint j=0;j<=i;j++)
// cout<<f[i][j]<<" ";
// cout<<endl;
// }
while(T--)
{
int n,m;
cin>>n>>m;
int ans=0;
for(fint i=0;i<=n;i++)
for(fint j=0;j<=min(i,m);j++)
if(f[i][j]%k==0)
ans++;
cout<<ans<<endl;
}
return 0;
}
```
该做法得分:70
**考虑正解做法**,所实话并不好想到:
先拿出柿子看一看:
我们要求的是$\large\sum _{i=0}^n\sum _{j=0}^{min(i,m)}K|C_j^i$
是否可以使用前缀和优化一下呢?
二维前缀和递推公式:$S_{i,j}=s_{i-1,j}+s_{i,j-1}-s_{i-1,j-1}+c_{i,j}$
在我那篇关于树状数组的博客讲解中有提及。
当我们预处理出组合数数组$C$时,直接让他$mod\ k$如果等于0那么对答案的贡献就$+1$,前缀和数组储存的是答案。那么整个递推式子就是:
```cpp
c[i][j]=(c[i-1][j]+c[i-1][j-1])%k;
s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+(c[i][j]==0);
s[i][i+1]=s[i][i];
```
该做法得分:100!!!
#### [60,花匠](https://www.luogu.com.cn/problem/P1970)
弱智DP。作为NOIP TG的Day2T1显然有些简单。
很容易想到用$f[i][1],f[i][0]$分别维护条件1和条件2的情况$1\to i$盆中最多保留的花盆数量,用$dp[i]$表示当前的最优保留数量,不难想到:
$f[i][1]=f[i-1][0]+1,f[i][0]=f[i-1][1]+1,dp[i]=max(f[i][0],f[i][1])$
最后结果即为$dp[n]$
然后实现一下即可。
代码:
```cpp
#include<bits/stdc++.h>
#define fint register int
#define h 5001
#define p 1489045
#define int long long
using namespace std;
int f[p][2],dp[p],a[p];
signed main()
{
int n;
cin>>n;
for(fint i=1;i<=n;i++)
cin>>a[i];
f[1][0]=f[1][1]=1;
for(fint i=2;i<=n;i++)
{
if(a[i]>a[i-1])
f[i][1]=f[i-1][0]+1,f[i][0]=f[i-1][0];
if(a[i]<a[i-1])
f[i][0]=f[i-1][1]+1,f[i][1]=f[i-1][1];
dp[i]=max(f[i][0],f[i][1]);
}
cout<<dp[n];
return 0;
}
```
然而只有80分,这是因为在$a[i]==a[i-1]$的时候状态转移断了
我们修改一下,加上
```cpp
if(a[i]==a[i-1])
f[i][0]=f[i-1][0],f[i][1]=f[i-1][1];
```
即可AC。
#### [61,Mashmokh and ACM](https://www.luogu.com.cn/problem/CF414B)
设$f_{i,j}$表示第$i$个数填$j$的方案数。枚举前一个数$l$,
那么显然$f_{i,j}+=f_{i-1,l}$
然而$O(n^3)$的算法效率过低。我们需要一些小小的优化!
当$j|l$时,显然我们可以知道$l*j$是小于$n$,那么状态转移方程就变成了:
$f[i][j]+=f[i-1][l*j]$
代码:
```cpp
#include<bits/stdc++.h>
#define fint register int
#define h 5001
#define N 4659465
using namespace std;
const int mods=1e9+7;
int f[h][h];
int main()
{
int n,k;
cin>>n>>k;
for(fint i=0;i<=n;i++)
f[1][i]=1;
for(fint i=2;i<=k;i++)
for(fint j=1;j<=n;j++)
for(fint l=1;j*l<=n;l++)
f[i][j]+=f[i-1][l*j],f[i][j]%=mods;
int ans=0;
for(fint i=1;i<=n;i++)
ans+=f[k][i],ans%=mods;
cout<<ans;
return 0;
}
```
还是可以的。
#### [62,最大正方形II](https://www.luogu.com.cn/problem/P1681)
求图中面积最大的交错正方形。
先来考虑求最大同色矩形的方案
题目在这:[最大正方形](https://www.luogu.com.cn/problem/P1387)
设状态$f[i][j]$表示在范围$(0,0)-(i,j)$范围覆盖点对$(i,j)$内的最大$1$矩形。
我们考虑转移:
当这个格子的数字为$1$的时候就可以转移。此时

我们显然需要从$A,B,C$这三个区域中选择一个去转移。此时由于新的矩形将覆盖整个$A,B,C$区域,所以需要在三种状态中选一个最小的做转移,然后能够形成面积$+1$的新矩形。那么假如此前三个位置结尾没有形成矩形,当前矩形面积$f[i][j]=1$
写成状态转移方程就是$f[i][j]=max\{f[i-1][j],f[i][j-1],f[i-1][j-1]\}+1$
那么回到本题,我们需要找到最大的交错正方形。,也就是0,1相间的矩形。
那么我们多开一个状态维护当前位置是0还是1
正如$f[i][j][0/1]$
轻松AC:
```cpp
int main()
{
int n,m;
cin>>n>>m;
for(fint i=1;i<=n;i++)
for(fint j=1;j<=m;j++)
cin>>a[i][j];
int ans=0;
for(fint i=1;i<=n;i++)
for(fint j=1;j<=m;j++)
{
if(a[i][j]==1)
f[i][j][1]=min(min(f[i-1][j][0],f[i][j-1][0]),f[i-1][j-1][1])+1;
else
f[i][j][0]=min(min(f[i-1][j][1],f[i][j-1][1]),f[i-1][j-1][0])+1;
ans=max(ans,max(f[i][j][0],f[i][j][1]));
}
cout<<ans;
return 0;
}
```
#### [63,雷涛的小猫](https://www.luogu.com.cn/problem/P1107)
设第$i$棵树$j$位置我们能得到最多的柿子为$f[i][j]$.
那么很容易设计一个状态转移方程:
$f[i][j]=max(f[i-1][j],f[i-delta][j+delta])+shizi[i][j]$
很遗憾,由于需要枚举$delta$也就是枚举从哪棵树转移最优,所以复杂度是$O(n^3)$的,所以这只是个部分分做法。
那么我们直接记录每个高度的最大收益,这样就少了一重枚举的循环,那不就妥妥的过了吗?
代码:
```cpp
int main()
{
int n,h,dt;
cin>>n>>h>>dt;
for(fint i=1;i<=n;i++)
{
cin>>num[i];
int hh;
for(fint j=1;j<=num[i];j++)
cin>>hh,shizi[i][hh]++;
}
int ans=0;
for(fint j=h;~j;j--)
for(fint i=1;i<=n;i++)
{
f[i][j]=max(f[i][j+1],dp[j+dt])+shizi[i][j];
dp[j]=max(dp[j],f[i][j]);
ans=max(f[i][j],ans);
}
cout<<ans;
return 0;
}
```
#### [64,A+B Problem Plus](https://www.luogu.com.cn/problem/P1832)
我连A+B都不会了,泪目。
首先我们要求出n以内素数的个数,并记录TA们
比如7=2+2+3=7=2+5;
那么很容易得到$dp[j]+=dp[j-su[i]]$.
这就转化成了背包问题。由于同一件物品可以多次选择,我们正序枚举
代码:
```cpp
signed main()
{
int n;
cin>>n;
oula(n);
f[0]=1;
for(fint i=1;i<=cnt;i++)
for(fint j=prime[i];j<=n;j++)//完全背包;
f[j]+=f[j-prime[i]];
cout<<f[n];
return 0;
}
inline void oula(int n)
{
vis[1]=1;
for(fint i=2;i<=n;i++)
{
if(!vis[i])
prime[++cnt]=i;
for(fint j=1;j<=cnt&&i*prime[j]<=n;j++)
{
vis[i*prime[j]]=1;
if(i%prime[j]==0)
break;
}
}
return ;
}
```
#### [65,路径统计2](https://www.luogu.com.cn/problem/P1176)
就是有两种走法,$m$个障碍,问走到一个点的方案数量.
很容易想到$dp[i][j]=dp[i-1][j]+dp[i][j-1]$
注意只有在没有障碍的时候才能转移。
代码:
```cpp
int main()
{
int n,m;
cin>>n>>m;
vis[1][1]=1;
int x,y;
for(fint i=1;i<=m;i++)
cin>>x>>y,vis[x][y]=1;
dp[1][1]=1;
for(fint i=1;i<=n;i++)
for(fint j=1;j<=n;j++)
if(!vis[i][j])
dp[i][j]=dp[i-1][j]+dp[i][j-1],dp[i][j]%=100003;
cout<<dp[n][n];
return 0;
}
```
#### [66,最大约数和](https://www.luogu.com.cn/problem/P1734)
选取不超过n个整数,那么选取的整数的数量和容量都是n,那么价值就是该数约数的和。
我们可以得到一个类似背包的转移:
$dp[j]=dp[j-i]+a[i];//a[i]$为$i$的约数的数量。
代码:
```cpp
int main()
{
int n;
cin>>n;
for(fint i=1;i<=n;i++)
a[i]=zheng(i);
for(fint i=1;i<=n;i++)
for(fint j=n;j>=i;j--)
f[j]=max(f[j-i]+a[i],f[j]);
cout<<f[n];
return 0;
}
inline int zheng(int x)
{
int ans=0;
for(fint i=1;i<x;i++)
if(x%i==0)
ans+=i;
return ans;
}
```
#### [67,Chain Reaction](https://www.luogu.com.cn/problem/CF607A)
某次CF,Div1的A题。
一直没看出来这题可以用DP来做。
其实理解了还行。
设$dp[i]$表示处理到位置$i$最大未被摧毁的数量。
本以为状态会从后往前$(len\to1)$转移,没想到是正着$(1\to len)$转移QAQ
设计完状态,那么其实就比较好写了:
很显然如果i位置没有灯塔,那么$dp[i]=dp[i-1]$
如果能覆盖整个左区间,那么$dp[i]=1$
其他情况则有他左区间左边那个点转移过来。
$dp[i]=dp[i-mp[i]-1]+1$
代码:
```cpp
int main()
{
int n;
cin>>n;
int len=0;
for(fint i=1;i<=n;i++)
cin>>a[i].pos>>a[i].dis,len=max(a[i].pos,len),mp[a[i].pos]=a[i].dis;
int ans=0;
if(mp[0])
dp[0]=1;
for(fint i=0;i<=len;i++)
{
if(!mp[i])
dp[i]=dp[i-1];
else
if(mp[i]>=i)
dp[i]=1;//一键摧毁只剩自己
else
dp[i]=dp[i-mp[i]-1]+1;
ans=max(ans,dp[i]);
}
cout<<n-ans;
return 0;
}
```
#### [68,绝世好题](https://www.luogu.com.cn/problem/P4310)
对于90%的数据,可以用$O(n^2)$的暴力水过,具体可参考最大上升子序列问题的做法:
$f[i]=max(f[i],f[j]+1)$
```cpp
signed main()
{
int n;
cin>>n;
for(fint i=1;i<=n;i++)
cin>>a[i];
for(fint i=1;i<=n;i++)
f[i]=1;
int ans=0;
for(fint i=2;i<=n;i++)
for(fint j=1;j<i;j++)
if(a[i]&a[j])
f[i]=max(f[i],f[j]+1),ans=max(ans,f[i]);
cout<<ans;
return 0;
}
```
#### [69,仓库建设](https://www.luogu.com.cn/problem/P2120)
很容易想到朴素的DP方程式:
$dp[i]=min\{dp[j]+P_k*|x_i-x_k|+C_i\}$
有点像是区间DP的亚子??
反正时间复杂度是$O(n^3)$,也就拿个暴力分QAQ。
暴力分打不满是件非常蓝瘦的事情。
比如说这份代码就只有11分(嘤嘤)
```cpp
int main()
{
int n;
cin>>n;
for(fint i=1;i<=n;i++)
cin>>x[i]>>p[i]>>c[i];
memset(f,0x3f,sizeof(f));
f[1]=0;
for(fint i=1;i<=n;i++)
{
for(fint j=1;j<i;j++)
for(fint k=j+1;k<i;k++)
f[i]=min(f[i],f[j]+p[k]*abs(x[k]-x[i]));
f[i]+=c[i];
}
cout<<f[n];
return 0;
}
```
我太菜了,萌新蒟蒻不会DP怎么办?在线等QAQ。
上面WA的原因就是我们没有更新每一个状态,输出中间变量我们就能发现$f[2]=0x3f$
怎么办呢?
不如把$f[0]=0$设为初始状态从0开始转移吧。
```cpp
int main()
{
int n;
cin>>n;
for(fint i=1;i<=n;i++)
cin>>x[i]>>p[i]>>c[i];
memset(f,0x3f,sizeof(f));
f[0]=0;
for(fint i=1;i<=n;i++)
{
for(fint j=0;j<i;j++)
{
int tot=0;
for(fint k=j+1;k<=i;k++)
tot+=p[k]*abs(x[k]-x[i]);
f[i]=min(f[i],f[j]+tot);
}
f[i]+=c[i];
}
cout<<f[n];
return 0;
}
/*
```
33分到手
我们还可以发现在中间的操作
```cpp
tot+=p[k]*(x[i]-x[k]);
```
貌似可以使用前缀和来维护。
怎么维护?
把柿子拆开:
$p[k]*x[i]-p[k]*x[k]$
分别维护一个$p$数组的前缀和和一个$p*x$数组的前缀和即可。
这样我们就有55分了(不开longlong只有44分)
```cpp
signed main()
{
// freopen("factory.in","r",stdin);
// freopen("factory.out","w",stdout);
int n;
cin>>n;
for(fint i=1;i<=n;i++)
{
cin>>x[i]>>p[i]>>c[i];
sc[i]=sc[i-1]+p[i]*x[i];
sp[i]=sp[i-1]+p[i];
}
memset(f,0x3f,sizeof(f));
f[0]=0;
for(fint i=1;i<=n;i++)
{
for(fint j=0;j<i;j++)
f[i]=min(f[i],f[j]+(sp[i-1]-sp[j])*x[i]-(sc[i-1]-sc[j]));
f[i]+=c[i];
}
cout<<f[n];
return 0;
}
```
PS:该做法未经过斜率优化,只有55pts
#### [70,杀蚂蚁](https://www.luogu.com.cn/problem/P2198)
一看就感觉是DP,但是数据范围又让人想到`__int128`(危)或者高精度。
于是选择先打暴力吧!毕竟能把暴力打稳打好也是一种本事呀(我fw,我不配)!
其实就是大力搜索就彳亍了。
最暴力的DFS:
```cpp
inline void dfs(int x,int now,int tot,int spd,int chi)//当前位置,放塔的类型,此时的总伤害,此时的速度,持续伤害
{
if(now==1)
tot+=spd*r;
tot+=chi*spd;
if(now==2)
chi+=g;
if(now==3)
spd+=b;
if(x==n)
{
ans=max(ans,tot);
return ;
}
for(fint i=1;i<=3;i++)
dfs(x+1,i,tot,spd,chi);
return ;
}
```
复杂度是$O(3^n)$,能拿10pts
分不多,也很好想,但是便于让我们想DP的状态
小贪心一波,由于干扰塔和放射塔是有后效性作用的,所以应该放在前面,而且干扰塔应该放在放射塔前面。
这一结论在搜索中不好在剪枝中运用,但是在DP中应该会很好用。
我们设$dp[i][j][k]$表示第$i$个位置有$j$个干扰塔$k$个放射塔,那么就要有$i-j-k$个激光塔。
初始状态$dp[1][1][0]=0,dp[1][0][1]=0,dp[1][0][0]=r$
我们试图压掉一维,那么$dp[i][j]$表示第$i$个位置放了$j$个干扰塔$i-j$个放射塔,后面$n-i$个位置全放激光塔。这种情况下蚂蚁爬到$i$位置受的伤害
柿子如下:
```cpp
f[i][j]=max(f[i-1][j-1]+g*(j-1)*(b*(i-j)+t),((i>j)?(f[i-1][j]+g*j*(b*(i-j-1)+t)):(0)));
```
当然不要忘记了最后要加上激光塔的伤害
```cpp
ans=max(ans,f[i][j]+(n-i)*(t+b*(i-j))*(g*j+r));
```
int128水过代码:
```cpp
#include<bits/stdc++.h>
#define fint register int
#define H 5001
#define N 4376894
#define int __int128
using namespace std;
int ans=0;
int n,r,g,b,t;
int f[H][H];
int read();
void print(__int128 x);
inline void sub_a();
inline void sub_b();
inline void dfs(int x,int now,int tot,int spd,int chi);
signed main()
{
n=read(),r=read(),g=read(),b=read(),t=read();
// if(n<=20)
// sub_a();
// else
sub_b();
return 0;
}
inline void dfs(int x,int now,int tot,int spd,int chi,int st,int ed)//当前位置,放塔的类型,此时的总伤害,此时的速度,持续伤害
{
if(now==1)
tot+=spd*r;
tot+=chi*spd;
if(now==2)
chi+=g;
if(now==3)
spd+=b;
if(x==n)
{
ans=max(ans,tot);
return ;
}
dfs(x+1,st,tot,spd,chi,st,ed);
dfs(x+1,ed,tot,spd,chi,st,ed);
return ;
}
inline void sub_a()
{
ans=0;
dfs(1,1,0,t,0,1,2);
dfs(1,2,0,t,0,1,2);
dfs(1,1,0,t,0,1,3);
dfs(1,3,0,t,0,1,3);
dfs(1,2,0,t,0,2,3);
dfs(1,3,0,t,0,2,3);
print(ans);
return ;
}
inline void sub_b()
{
ans=0;
for(fint i=1;i<=n;i++)
for(fint j=1;j<=i;j++)
f[i][j]=max(f[i-1][j-1]+g*(j-1)*(b*(i-j)+t),((i>j)?(f[i-1][j]+g*j*(b*(i-j-1)+t)):(0)));
for(fint i=0;i<=n;i++)
for(fint j=0;j<=i;j++)
ans=max(ans,f[i][j]+(n-i)*(t+b*(i-j))*(g*j+r));
print(ans);
return ;
}
int read()
{
int x=0,k=1;char ch=' ';
while(!isdigit(ch)){
ch=getchar();
if(ch=='-') k=-1;
}
while(isdigit(ch)){
x=x*10+ch-'0';
ch=getchar();
}
return k*x;
}
void print(__int128 x)
{
if(x>9) print(x/10);
putchar(x%10+'0');
}
```
#### [71,Tetrahedron](https://www.luogu.com.cn/problem/CF166E)
相对来说算是比较水的。和几何相关的那种,由于状态单一(步数),而且数据范围较大($1e7$)所以我们肯定使用一维DP来解决。
那么我们设$f[i]$表示走了$i$步的方案数。
比如说从D出发,走1步,可以走到A,B,C三个位置,方案数三种,其中能回到原点的有零种.
走两步,可以走DAB,DAC,DBC,DBA,DCB,DCA,DAD,DBD,DCD9个方案,其中回到原点的三种.
先分类讨论,用$f[i][0],f[i][1]$分别表示回不到原点的方案数和能回的方案数。
我们记录$f[1][0]=3,f[1][1]=0,f[2][0]=6,f[2][1]=3$
继续手算:
$f[3][0]=27,f[3][1]=6$
由于每一步都可以走向除自身外三个位置的任一个,
所以可以很轻易推出来,走$n$步的总方案数是$3^{n}$种,其中回到原点的有$3^{n-1}-3^{n-2}$种
我们把第二维压掉,也就是只考虑能回到原点的情况
也就是说$f[i]=3^{i-1}-f[i-1]$
那么硬艹就完了。
代码:
```cpp
#include<bits/stdc++.h>
#define fint register int
#define int long long
#define N 11347845
#define H 5001
using namespace std;
const int mods=1e9+7;
int f[N];
signed main()
{
int n;
cin>>n;
f[1]=0;
int bas=3;
for(fint i=2;i<=n;i++)
{
f[i]=bas-f[i-1];
f[i]=(f[i]%mods+mods)%mods;
bas*=3LL;
bas%=mods;
}
cout<<f[n];
return 0;
}
```
#### [72,数的划分](https://www.luogu.com.cn/problem/P1025)
偶然发现还有这样一道黄DP没有写,赶紧来解决它。
话说数据范围这么小,大力搜索也完全可过丫。
我们设立状态$dp[i][j]$表示$i$个数分为$j$组的方案数
那么我们可以从同样的组少一个数的状态即$dp[i-j][j]$继承过来,此时该位置选$j$,也可以从这一组选$1$来转移,那么柿子就是$dp[i-1][j-1]$
代码:
```cpp
int main()
{
int n,k;
cin>>n>>k;
for(fint i=1;i<=n;i++)
f[i][1]=1;
for(fint i=1;i<=n;i++)
for(fint j=2;j<=k;j++)
if(i>=j)
f[i][j]=f[i-1][j-1]+f[i-j][j];
cout<<f[n][k];
return 0;
}
```
#### [73,球迷购票问题](https://www.luogu.com.cn/problem/P1754)
设$dp[i][j]$表示前面$i$个人有$j$张50
那么$dp[i][j]=dp[i-1][j-1]$//第$i$个人拿的$50$
$dp[i][j]+=dp[i-1][j+1]$//第$i$个人拿的$100$需要找一张$50$
代码:
```cpp
signed main()
{
int n;
cin>>n;
f[0][0]=1;
for(fint i=1;i<=(n<<1);i++)
for(fint j=0;j<=n&&j<=i;j++)
if(j!=0)
f[i][j]+=f[i-1][j-1]+f[i-1][j+1];
else
f[i][j]+=f[i-1][j+1];
cout<<f[n<<1][0];
return 0;
}
```
#### [74,三素素数](https://www.luogu.com.cn/problem/P2359)
一道基础的DP题,模拟赛是做到了。来发一波题解。
我们可以开一个三维的数组f[t][i][j],i表示n位数,j表示此时末位数,i表示末位数前一位数,进行三层循环
**预处理**
```cpp
inline void pre()
{
for(fint i=0;i<=9;i++)
for(fint j=0;j<=9;j++)
{
for(fint k=1;k<=9;k++)
if(Pri(k*100+j*10+i))
f[3][i][j]=++cnt;
cnt=0;
}
return ;
}
```
**转移方程**
```cpp
for(fint T=4;T<=n;T++)
for(fint i=0;i<=9;i++)
for(fint j=0;j<=9;j++)
for(fint k=1;k<=9;k++)
if(Pri(k*100+j*10+i))
f[T][i][j]=(f[T][i][j]+f[T-1][j][k]);
```
**注意**:很多题解在循环上都是1-9,这是不对的,因为预处理后当输入3,结果是128,而正确答案是134.
最后上完整代码:
```cpp
signed main()
{
//freopen("threeprime.in","r",stdin);
//freopen("threeprime.out","w",stdout);
cin>>n;
pre();
pd(n);
cout<<ans%mods;
return 0;
}
inline void pd(int n)
{
for(fint T=4;T<=n;T++)
for(fint i=0;i<=9;i++)
for(fint j=0;j<=9;j++)
for(fint k=1;k<=9;k++)
if(Pri(k*100+j*10+i))
f[T][i][j]=(f[T][i][j]+f[T-1][j][k])%mods;
for(fint i=0;i<=9;i++)
for(fint j=0;j<=9;j++)
ans+=f[n][i][j],f[n][i][j]%=mods;
return ;
}
inline bool Pri(int x)
{
if(x==0||x==1)
return 0;
if(x==2||x==3)
return 1;
if(x%6!=5&&x%6!=1)
return 0;
for(fint i=5;i<=sqrt(x);i++)
if(x%i==0||x%(i+2)==0)
return 0;
return 1;
}
inline void pre()
{
for(fint i=0;i<=9;i++)
for(fint j=0;j<=9;j++)
{
for(fint k=1;k<=9;k++)
if(Pri(k*100+j*10+i))
f[3][i][j]=++cnt;
cnt=0;
}
return ;
}
```
## 区间DP问题(7道)
#### [1,篮球比赛1](http://hzwer.com/5053.html)
预处理所有异或和及与和,枚举断点即可。
```cpp
int main()
{
int n;
cin>>n;
int maxxs=0;
for(fint i=1;i<=n;i++)
cin>>a[i];
for(fint i=1;i<n;i++)
{
for(fint j=0;j<2048;j++)
x[i][j]=sa[j^a[i]],x[i][j]%=mods;//求出前i位异或值为j的方案。
x[i][a[i]]++;//自己本身免异或产生自己
x[i][a[i]]%=mods;
for(fint j=0;j<2048;j++)
sa[j]+=x[i][j],sa[i]%=mods;
}
for(fint i=n-1;i>=1;i--)
{
for(fint j=0;j<2048;j++)
an[i][j]=sb[j&a[i]],an[i][j]%=mods;//求出前i位按位与值为j的方案。
an[i][a[i]]++;//自己本身免与即可产生自己
an[i][a[i]]%=mods;
for(fint j=0;j<2048;j++)
sb[j]+=an[i][j],sb[i]%=mods;
}
int ans=0;
for(fint i=1;i<n;i++)
for(fint j=0;j<2048;j++)
ans+=(sa[j]*an[i+1][j]),ans%=mods;
cout<<ans;
return 0;
}
```
#### [2,石子合并](https://www.luogu.com.cn/problem/P1880)
第一维枚举区间长度,第二维枚举左端点,右端点即为$i+len-1$.
状态转移方程很显然$f_{i,j}=f_{i,k}+f_{k+1,j}$
DP
```cpp
for(fint len=2;len<=n;len++)//枚举区间长度
for(fint i=1;i<n;i++)//枚举左端点
{
int j=i+len-1;//求得len长度下的右端点
for(fint k=i;k<j;k++)//枚举中间断点
f[i][j]=max(f[i][j],f[i][k]+f[k+1][j]+s[i][j]);
}
```
记忆化搜索
```cpp
inline int mfsa(int l,int r)
{
if(l==r)
return fa[l][r]=0;
if(fa[l][r]!=0)
return fa[l][r];
int maxa=0;
for(fint i=l;i<r;i++)
maxa=max(maxa,mfsa(l,i)+mfsa(i+1,r)+s[r]-s[l-1]);
return fa[l][r]=maxa;
}
inline int mfsb(int l,int r)
{
if(l==r)
return fb[l][r]=0;
if(fb[l][r]!=inf)
return fb[l][r];
int mina=inf;
for(fint i=l;i<r;i++)
mina=min(mina,mfsb(l,i)+mfsb(i+1,r)+s[r]-s[l-1]);
return fb[l][r]=mina;
}
```
#### [3,能量项链](https://www.luogu.com.cn/problem/P1063)
DP
```cpp
for(fint i=1;i<=n;i++)
cin>>a[i],a[i+n]=a[i];//化环为链
for(fint len=2;len<=n*2;len++)
for(fint i=1;i+len-1<=n;i++)
{
int j=i+len-1;
for(fint k=i+1;k<j;k++)
f[i][j]=max(f[i][k]+f[k][j]+a[i]*a[j]*a[k],f[i][j]);
}
```
#### [4,涂色](https://www.luogu.com.cn/problem/P4170#submit)
记忆化搜索
```cpp
inline int dfs(int l,int r)
{
if(r<l)
return 0;
if(f[l][r]!=1061109567)
return f[l][r];
if(a[l]==a[r])
f[l][r]=min(dfs(l+1,r),dfs(l,r-1));
for(fint i=l;i<r;i++)
f[l][r]=min(dfs(l,i)+dfs(i+1,r),f[l][r]);
return f[l][r];
}
```
#### [5,合唱队](https://www.luogu.com.cn/problem/P3205#submit)
记忆化搜索
```cpp
inline int dfs(int l,int r,int x)
{
if(r<l)
return 0;
if(f[l][r][x]!=-1)
return f[l][r][x];
int ans=0;
if(a[l+1]>a[l]&&x==0)
ans+=dfs(l+1,r,0);
if(a[r]>a[l]&&x==1)
ans+=dfs(l,r-1,0);
if(a[r]>a[l]&&x==0)
ans+=dfs(l+1,r,1);
if(a[r]>a[r-1]&&x==1)
ans+=dfs(l,r-1,1);
f[l][r][x]=ans%mods;
return f[l][r][x];
}
```
#### [6,关路灯](https://www.luogu.com.cn/problem/P1220)
DP
```cpp
for(fint len=1;len<n;len++)
for(fint i=1;i+len-1<=n;i++)
{
int j=i+len-1;
f[i-1][j][0]=min(f[i-1][j][0],min(f[i][j][0]+(pos[i]-pos[i-1])*(s[i-1]+s[n]-s[j]),f[i][j][1]+(pos[j]-pos[i-1])*(s[i-1]+s[n]-s[j])));
f[i][j+1][1]=min(f[i][j+1][1],min(f[i][j][1]+(pos[j+1]-pos[j])*(s[i-1]+s[n]-s[j]),f[i][j][0]+(pos[j+1]-pos[i])*(s[i-1]+s[n]-s[j])));
}
```
#### [7,删数](https://www.luogu.com.cn/problem/P2426)
区间DP问题。虽然是个黄题,但也没有一眼秒那么简单。
好久没有做区间DP了,做起来有些手生~~(就是菜。。~~
先来考虑状态的设计:
我们设$f[i][j]$为当前需要删区间$[i,j]$时的方案数。
但是我们并不知道这次删数的区间长度,因为我们要求从左边或右边去掉连续的$i(1≤i≤n)$个数所以这时候我们就需要枚举区间。
很容易得到状态转移方程式$f[i][j]=max(f[i][k]+f[i+1][j],f[i][j])$
然后很容易的打出这样的代码:
```cpp
for(fint i=1;i<=n;i++)
for(fint j=i+1;j<=n;j++)
{
f[i][j]=abs(a[i]-a[j])*(j-i+1);
for(fint k=i;k<j;k++)
f[i][j]=max(f[i][k]+f[k+1][j],f[i][j]);
}
```
但是,这并不对,因为这样做并不满足DP的无后效性原则。
我们$f[i][j]$可能会从一个$k,k>i$的状态转移过来,而假如此时还未枚举到这种状态,显然会发生错误,这就需要我们从大到小$i$,从小往大枚举$j$
由此得到AC代码:
```cpp
int main()
{
int n;
cin>>n;
for(fint i=1;i<=n;i++)
cin>>a[i],f[i][i]=a[i];
for(fint i=n;i;i--)
for(fint j=i+1;j<=n;j++)
{
f[i][j]=abs(a[i]-a[j])*(j-i+1);
for(fint k=i;k<j;k++)
f[i][j]=max(f[i][k]+f[k+1][j],f[i][j]);
}
cout<<f[1][n];
return 0;
}
```
## 树上/图上DP问题(6道)
#### [1,最大食物链计数](https://www.luogu.com.cn/problem/P4017)
先topu,然后:
$f_i+=f_{j},j∈in[j]=0$
```cpp
signed main()
{
ios::sync_with_stdio(false);
int n,m;
n=read(),m=read();
int x,y;
for(fint i=1;i<=m;i++)
x=read(),y=read(),in[y]++,ou[x]++,adds(x,y);
for(fint i=1;i<=n;i++)
if(!in[i])
q.push(i),f[i]=1;
for(fint i=1;i<=n;i++)
while(!q.empty())
{
int hea=q.front();
q.pop();
for(fint i=head[hea];i;i=e[i].nxt)
{
in[e[i].to]--,f[e[i].to]+=f[hea],f[e[i].to]%=mods;
if(!in[e[i].to])
q.push(e[i].to);
}
}
int ans=0;
for(fint i=1;i<=n;i++)
if(!ou[i])
ans+=f[i],ans%=mods;
cout<<ans;
return 0;
}
```
#### [2,Friends](https://atcoder.jp/contests/abc177/tasks/abc177_d)
算是个简单的树上DP(或者说是带权并查集?)
由于我朋友的朋友也是我的朋友,所以考虑用并查集维护同一个朋友圈为一棵树
对于每次合并根节点为$i,j$的两棵树,我们可以得到递推式:
$dp_{root_i}+=dp_{root_j}$
找根操作可以通过并查集一步到位!
```cpp
int main()
{
ios::sync_with_stdio(false);
int n,m;
cin>>n>>m;
for(fint i=1;i<=n;i++)
f[i]=i,siz[i]=1;
int x,y;
for(fint i=1;i<=m;i++)
cin>>x>>y,unions(x,y);
int ans=0;
for(fint i=1;i<=n;i++)
ans=max(siz[i],ans);
cout<<ans;
return 0;
}
inline int findx(int x)
{
if(f[x]==x)
return x;
return f[x]=findx(f[x]);
}
inline void unions(int x,int y)
{
int fx=findx(x),fy=findx(y);
if(fx!=fy)
f[fx]=fy,siz[fy]+=siz[fx];
return ;
}
```
#### [3,信息传递](https://www.luogu.com.cn/problem/P2661)
当$i,x$不在同一个连通分量里时,我们记录i,x所在联通分量中合并的步数和
$dp[x]+=dp[f[x]];$
然后更新:$dp[i]=dp[x]+1$,
否则就是已经OK,我们更新最小值即可。
代码:
```cpp
int main()
{
int n;
cin>>n;
for(fint i=1;i<=n;i++)
f[i]=i;
int minns=56839464;
int x;
for(fint i=1;i<=n;i++)
{
cin>>x;
if(findx(i)!=findx(x))
dp[i]=dp[x]+1,f[findx(i)]=findx(x);
else
minns=min(minns,dp[x]+1);
}
cout<<minns;
return 0;
}
inline int findx(int x)
{
if(f[x]==x)
return x;
int now=f[x];
f[x]=findx(f[x]);
dp[x]+=dp[now];
return f[x];
}
```
#### [4,银河英雄传说](https://www.luogu.com.cn/problem/P1196)
裸的带权并查集。在合并时进行更新。
```cpp
for(fint i=1;i<=30001;i++)
f[i]=i,num[i]=1;
for(fint i=1;i<=n;i++)
{
cin>>cha;
if(cha=='M')
cin>>a>>b,unions(a,b);
else
cin>>a>>b,cout<<judge(a,b)<<endl;
}
inline int findx(int x)
{
if(f[x]==x)
return x;
int fs=findx(f[x]);
line[x]+=line[f[x]];
return f[x]=fs;
}
inline void unions(int x,int y)
{
int xa=findx(x),ya=findx(y);
if(xa==ya)
return ;
line[xa]+=num[ya];
f[xa]=ya;
num[ya]+=num[xa];
num[xa]=0;
return ;
}
```
#### [5.括号树](https://www.luogu.com.cn/problem/P5658)
首先看到括号串就想到要用栈(条件反射???)不多说,先读题:
**合法括号串 **
`()`是一个合法括号串
`(())`是两个合法括号串,但是对于第一个`)`而言只有一个合法匹配,对于第二个`)`而言也只有一个合法匹配。
`(())`对于第一个`)`有两个合法匹配,对于第二个`)`也有两个合法匹配。
**不同的括号串**
`S` 的两个子串视作不同**当且仅当**它们在 `S` 中的位置不同,即 $l$不同或 $r$ 不同
不难想到用DP来解决。
再来看数据:
- 前$2$个点在链上且$n≤$8
这部分我们可以用暴力来解决,复杂度$O(n^4)$
```cpp
inline void sub_violence()
{
for(fint i=2;i<=n;i++)//根到第i号节点的路径上
{
for(fint l=1;l<=i;l++)//枚举区间左端点
for(fint r=l+1;r<=i;r++)//枚举区间右端点
{
int L=0,R=0;
for(fint j=l;j<=r;j++)//区间内括号匹配
{
if(a[j]=='(')
L++;
else
if(a[j]==')')
R++;
if(R>L)
break;
}
if(L==R)
c[i]++;
}
}
int ans=0;
for(fint i=2;i<=n;i++)
ans^=c[i]*i;
cout<<ans;
return ;
}
```
- 接下来,考虑55分的链上做法:
开一个栈储存左括号,当遇到右括号时如果栈中没有左括号,那显然无法匹配。如果栈中有左括号,我们从栈顶的前一个位置递推转移过来。为什么呢?
因为对于括号匹配来说,优先匹配离他近的括号,如果一个左括号出栈了,那就证明从这个左括号到后面的右括号中间没有别的左括号,而此时我们新增一个匹配的括号,然而我们需要求得是$1$~$i$中这条路径上有多少括号匹配完全了。所以,我们要从该匹配左括号前面的一个位置做一个前缀和更新当前从$1$到$i$总的匹配数,最后用$c$数组记录从$1\to $,而$i$中有c[i]个不同子串是合法的。因为我们枚举的是i位置为`)`才可能产生匹配,这种匹配一定是新的区间的匹配。显然$c[i]=c[i-1]+s[i]$
代码:
```cpp
if(a[1]=='(')
st[++tops]=1;
for(fint i=2;i<=n;i++)//在从1到i的路径上
{
if(a[i]=='(')
st[++tops]=i;
else
if(a[i]==')'&&tops)
s[i]=s[st[tops--]-1]+1;
c[i]=c[i-1]+s[i];
}
int ans=0;
for(fint i=2;i<=n;i++)
ans^=c[i]*i;
cout<<ans;
```
或许我们将这种操作转移到树上在$dfs$的过程进行,也能拿分。
只不过状态转移方程需要改变了。由于在一颗树上无法保证节点的连续性,我们不能继续用$S_{i}=S_{st[tops--]-1}+1$的转移了。但是,我们仍可以记录转移位置$last$,那么状态就变成了$S_i=S_{fa[last[i]]}+1$,道理都是一样滴。那么最后答案的转移,$C_i=C_{fa[i]}+S_i$.那么问题来了,如何找到一个位置的$last$函数呢?当$i$为`(`时,$last_i=i$否则$last_i=last_{fa[i]}$
那么考虑代码实现:
```cpp
inline void sub_tree()
{
for(fint i=1;i<=n;i++)
{
int fa=f[i];
las[i]=las[fa];
if(a[i]=='(')
las[i]=i;
else
if(a[i]==')'&&las[i])
s[i]=s[f[las[i]]]+1,las[i]=las[f[las[i]]];
c[i]=c[fa]+s[i];
}
int ans=0;
for(fint i=2;i<=n;i++)
ans^=c[i]*i;
cout<<ans;
return ;
}
```
说实话正解并不是很好想,但是和链上部分做法到是也差不多,
期望得分:$50\to55$
期望时间:$1.5hour$
完整代码:
```cpp
#include<bits/stdc++.h>
#define fint register int
#define h 5001
#define p 1437558
#define int long long
using namespace std;
char a[p];
int f[p],c[p],st[p],tops=0,s[p],las[p];
int n;
inline void sub_tree();
inline void sub_chain();
inline void sub_violence();
signed main()
{
freopen("brackets.in","r",stdin);
freopen("brackets.out","w",stdout);
cin>>n;
scanf("%s",a+1);
int tot=0;
for(fint i=2,j=0;i<=n;i++)
cin>>f[i],f[i]==i-1?tot++:j++;
if(tot==n-1)
sub_chain();
else
sub_tree();
return 0;
}
inline void sub_chain()
{
if(n<=8)
sub_violence();
else
{
if(a[1]=='(')
st[++tops]=1;
for(fint i=2;i<=n;i++)//在从1到i的路径上
{
if(a[i]=='(')
st[++tops]=i;
else
if(a[i]==')'&&tops)
s[i]=s[st[tops--]-1]+1;
c[i]=c[i-1]+s[i];
}
int ans=0;
for(fint i=2;i<=n;i++)
ans^=c[i]*i;
cout<<ans;
}
return ;
}
inline void sub_violence()
{
for(fint i=2;i<=n;i++)//根到第i号节点的路径上
{
for(fint l=1;l<=i;l++)//枚举区间左端点
for(fint r=l+1;r<=i;r++)//枚举区间右端点
{
int L=0,R=0;
for(fint j=l;j<=r;j++)//区间内括号匹配
{
if(a[j]=='(')
L++;
else
if(a[j]==')')
R++;
if(R>L)
break;
}
if(L==R)
c[i]++;
}
}
int ans=0;
for(fint i=2;i<=n;i++)
ans^=c[i]*i;
cout<<ans;
return ;
}
inline void sub_tree()
{
for(fint i=1;i<=n;i++)
{
int fa=f[i];
las[i]=las[fa];
if(a[i]=='(')
las[i]=i;
else
if(a[i]==')'&&las[i])
s[i]=s[f[las[i]]]+1,las[i]=las[f[las[i]]];
c[i]=c[fa]+s[i];
}
int ans=0;
for(fint i=2;i<=n;i++)
ans^=c[i]*i;
cout<<ans;
return ;
}
```
#### [6,恋爱](https://www.luogu.com.cn/problem/P3408)
首先,这肯定是个以0为根的树形结构,我们使用临接表建树,并记录下每个节点儿子的个数。
也就是这样
```cpp
for(fint i=1;i<=n;i++)
cin>>b>>a[i],adds(b,i),adds(i,b),son_num[b]++;
```
然后以0为根进行DFS操作。
此时分类讨论:
- 对于叶子节点,我们一定要给他钱,这样才能满足写信的条件
- 对于非叶结点,由于小B的直属下属有不小于T分之C的人写信表示小A向小B求爱,那么她会同意小A的请求写信。所以我们选择最小的$a[x]*son_num[x]/t$给钱。
此时的花费就是最小的。
由此可以得到DP方程式:
$dp[i]+=dp[sons[i]];(i!=leaf)$
$dp[i]+=a[x](i==leaf)$
那么如何选择最小的$a[x]*son_num[x]/t$花费呢?
我们可以考虑排序。但是对于邻接表的结构而已,sort起来并不方便,所以我们选择使用小根堆,把亲儿子节点(直属下司)按DP值进行排序,并加入堆,并取出最小的$a[x]*son_num[x]/t+1$个即可。
```cpp
priority_queue <int,vector<int>,greater<int> >q;
for(fint i=head[x];i;i=e[i].nxt)
if(e[i].to!=fa)
q.push(dp[e[i].to]);
```
然后我们按照状态转移方程式更新即可。
对于非叶节点:
```cpp
for(fint i=1;i<=son_num[x]&&i<=(int)((double)a[x]*son_num[x]/t+1)&&q.size();i++)
dp[x]+=q.top(),q.pop();
```
对于叶子节点:
```cpp
if(!son_num[x])
{
dp[x]+=a[x];
return ;
}
```
最后结果就是:
```cpp
cout<<dp[0];
```
完整注释代码:
```cpp
#include<bits/stdc++.h>
#define fint register int
#define H 5001
#define N 4375089
#define int long long
#define _fxxk cout<<"ZGW AK IOI"
using namespace std;
struct node
{
int to;
int nxt;
}
e[N];
int cnt;
int head[N];
int n,t,c;
int a[N],son_num[N],dp[N];
inline void adds(int u,int v);
inline void dfs(int x,int fa);
signed main()
{
// freopen("love.in","r",stdin);
// freopen("love.out","w",stdout);
cin>>n>>t>>c;
int b;
a[0]=c;
for(fint i=1;i<=n;i++)
cin>>b>>a[i],adds(b,i),adds(i,b),son_num[b]++;//存图
// for(fint i=0;i<=n;i++)
// cout<<son_num[i]<<" ";
dfs(0,n+1);
cout<<dp[0];
return 0;
}
inline void adds(int u,int v)
{
e[++cnt].to=v;
e[cnt].nxt=head[u];
head[u]=cnt;
return ;
}
inline void dfs(int x,int fa)
{
if(!son_num[x])//叶子节点有爹没儿子
{
dp[x]+=a[x];//那就直接掏钱吧
//_fxxk;
return ;
}
for(fint i=head[x];i;i=e[i].nxt)
if(e[i].to!=fa)
dfs(e[i].to,x);
priority_queue <int,vector<int>,greater<int> >q;//临界表不好排序,那就用堆艹
for(fint i=head[x];i;i=e[i].nxt)
if(e[i].to!=fa)
q.push(dp[e[i].to]);
// cout<<((double)a[x]*son_num[x]/t)<<" ";
for(fint i=1;i<=son_num[x]&&i<=(int)((double)a[x]*son_num[x]/t+1)&&q.size();i++)
dp[x]+=q.top(),q.pop();
// cout<<dp[x]<<" ";
return ;
}
```
## 状态压缩DP问题(1道)
#### [1,关灯问题 II](https://www.luogu.com.cn/problem/P2622)
蒟蒻的第一道状压题。
初始所有灯均开着,二进制位均为1,即$(1<<n)-1$
当1操作且灯开着的时候,就关上:
$if(s\&(1<<(j-1)))\ \ s\ xor=(1<<j-1)$
当-1操作且灯关着的时候,就打开:
$if(!(s\&(1<<(j-1)))\ \ s\ xor=(1<<j-1)$
代码:
```cpp
int main()
{
ios::sync_with_stdio(false);
int n,m;
cin>>n>>m;
for(fint i=1;i<=m;i++)
for(fint j=1;j<=n;j++)
cin>>a[i][j];
queue <node>q;
q.push((node){(1<<n)-1,0});//初始二进制位全为1
vis[(1<<n)-1]=1;
bool ff=0;
while(!q.empty())
{
node hea=q.front();
q.pop();
if(hea.now==0)
{
cout<<hea.stp,ff=1;
break;
}
for(fint i=1;i<=m;i++)
{
int s=hea.now;
for(fint j=1;j<=n;j++)
if(a[i][j]==1&&(s&(1<<(j-1))))
s^=(1<<(j-1));//如果开了就关上
else
if(a[i][j]==-1&&!(s&(1<<(j-1))))
s^=(1<<(j-1));//如果关了就打开
if(!vis[s])
vis[s]=1,q.push((node){s,hea.stp+1});
}
}
if(!ff)
cout<<-1;
return 0;
}
```
## 概率/期望DP问题(2道)
#### [1,Crossing Rivers](https://www.luogu.com.cn/problem/UVA12230)
先以一道不是DP的题目开始吧。来熟悉一下期望问题吧
过河的最坏时间是$\frac{3L}v$,最好时间是$\frac{L}v$,线性分布下两种情况的概率均约为$\frac 12$,那么总体的期望时间就是$\frac {2L}v$
代码:
```cpp
int main()
{
int Case=0;
while(1)
{
double ans=0.00;
int n,d;
cin>>n>>d;
if(n==0&&d==0)
break;
int p,l,v;
for(fint i=1;i<=n;i++)
{
cin>>p>>l>>v;
ans+=(double)(2*l)/v;
d-=l;
}
ans+=(double)d;
printf("Case %d: %.3lf\n\n",++Case,ans);
}
return 0;
}
```
#### [2,Favorite Dice](https://www.luogu.com.cn/problem/SP1026)
很经典的问题呀。
我们设$dp[i]$表示掷到了$i$面筛子,还期望再弄$dp[i]$次的期望。
我们有$\frac in$的概率能掷到相同的的面,此时相当于白弄了,还需要$dp[i]$次,也就是$\frac in*dp[i]$;
还有$\frac {(n-i)}n$的概率掷到了新的一面,此时期望仍需要掷的次数变成了$dp[i+1]$
所以可以推得柿子:
$dp[i]=dp[i]*\frac in+\frac {(n-i)}n*dp[i+1]$
化简一下,变成:
$dp[i]=\frac n{(n-i)}+dp[i+1]$
代码:
```cpp
int main()
{
int T;
cin>>T;
while(T--)
{
memset(dp,0,sizeof(dp));
int n;
cin>>n;
dp[n]=0.0000;
for(fint i=n-1;i>=0;i--)
dp[i]=dp[i+1]+(double)((double)n/(n-i));
printf("%.2lf\n",dp[0]);
}
return 0;
}
```
## DP优化问题(10道)
#### [1,斐波那契数列](https://www.luogu.com.cn/problem/P1962)
原矩阵:
`1 1`
`1 0`
```cpp
struct node
{
int a[h][h];
}
B,Ans;
int n=2,kk;
node operator *(const node &x,const node &y)
{
node f;
for(fint i=1;i<=n;i++)
for(fint j=1;j<=n;j++)
f.a[i][j]=0;
for(fint i=1;i<=n;i++)
for(fint j=1;j<=n;j++)
for(fint k=1;k<=n;k++)
f.a[i][j]+=x.a[i][k]*y.a[k][j]%mods,f.a[i][j]%=mods;
return f;
}
inline int read();
signed main()
{
cin>>kk;
for(fint i=1;i<=n;i++)
for(fint j=1;j<=n;j++)
Ans.a[i][j]=0,B.a[i][j]=0;
B.a[1][1]=B.a[1][2]=B.a[2][1]=1;
for(fint i=1;i<=n;i++)
Ans.a[i][i]=1;
while(kk>0)
{
if(kk&1)
Ans=Ans*B;
B=B*B;
kk>>=1;
}
cout<<Ans.a[2][1]<<endl;
return 0;
}
```
#### [2,矩阵加速](https://www.luogu.com.cn/problem/P1939)
原矩阵:
```
1 0 1
1 0 0
0 1 0
```
```cpp
struct node
{
int a[10][10];
}b,ans;
int n;
inline node ksm(node aa,node bb);
signed main()
{
ios::sync_with_stdio(false);
int T;
cin>>T;
while(T--)
{
cin>>n;
for(fint i=1;i<=3;i++)
for(fint j=1;j<=3;j++)
ans.a[i][j]=0,b.a[i][j]=0;
b.a[1][1]=1,b.a[2][1]=1,b.a[3][2]=1,b.a[1][3]=1;
for(fint i=1;i<=3;i++)
ans.a[i][i]=1;
int pp=n;
while(pp>0)
{
if(pp%2==1)
ans=ksm(ans,b);
b=ksm(b,b);
pp>>=1;
}
cout<<ans.a[2][1]<<endl;
}
return 0;
}
inline node ksm(node aa,node bb)
{
node f;
for(fint i=1;i<=3;i++)
for(fint j=1;j<=3;j++)
f.a[i][j]=0;
for(fint i=1;i<=3;i++)
for(fint j=1;j<=3;j++)
for(fint k=1;k<=3;k++)
f.a[i][j]+=aa.a[i][k]*bb.a[k][j],f.a[i][j]%=mods;
return f;
}
```
#### [3,回文字串](https://www.luogu.com.cn/problem/P1435)
在此前的线性DP环节,我们已经体验过这题的解法了,然而空间属实有点小大。
所以我们需要用滚动数组进行优化。
我们其实还可以使用滚动数组压掉一维。
用$dp_j$记录前一种情况,即$f_{i-1,j}$,$f_j$则记录二维时$f_{i,j}$的情况
然后得到转移方程:
```cpp
for(fint i=1;i<=len;i++)
for(fint j=1;j<=len;j++)
if(a[i]==b[j])
f[j]=dp[j-1]+1;
else
f[j]=max(f[j-1],dp[j]);
```
最后把f数组赋给dp数组在i往后退时使用
```cpp
memcpy(dp,f,sizeof(f));
```
#### [4,宝物筛选](https://www.luogu.com.cn/problem/P1776)
二进制拆分多重背包的典例QWQ。
具体方式就是把多个价值相同的物品拆成不同价值的物品,这样空间复杂度增加了,时间复杂度却降低了。
举个例子:`3,9,6`
拆成$3×2^0,3×2^0$,剩余数量为5
$3×2^1,9×2^1$,剩余数量为3
下面c小于2^2,拆不成2进制了,直接拆c清零
$3×3,9×3$剩余数量为0
这样就被拆成了3件不同的物品。
```cpp
int main()
{
int n,W;
cin>>n>>W;
int a,b,c;
int cnt=0;
for(fint i=1;i<=n;i++)
{
cin>>a>>b>>c;
for(fint j=1;j<=c;j<<=1)
v[++cnt]=j*a,w[cnt]=j*b,c-=j;
if(c)
v[++cnt]=c*a,w[cnt]=c*b;
}
for(fint i=1;i<=cnt;i++)
for(fint j=W;j>=w[i];j--)
f[j]=max(f[j],f[j-w[i]]+v[i]);
cout<<f[W];
return 0;
}
```
#### [5,樱花](https://www.luogu.com.cn/problem/P1833)
二进制拆分一下,然后就是一个简单的混合背包。记得把完全背包和多重背包分开跑,或者说把完全背包容量定为一个大数(如99999).
```cpp
int main()
{
// freopen("C.in","r",stdin);
// freopen("C.out","w",stdout);
int ha,ma,hb,mb,n;
scanf("%d:%d%d:%d%d",&ha,&ma,&hb,&mb,&n);
int tim=(hb-ha)*60+(mb-ma);
//cout<<t;
for(fint i=1;i<=n;i++)
cin>>t[i]>>c[i]>>p[i];
int cnt=0;
for(fint i=1;i<=n;i++)
{
int now=p[i];
if(now!=0)
for(fint j=1;j<=now;j<<=1)
ta[++cnt]=t[i]*j,ca[cnt]=c[i]*j,now-=j;
if(now>0)
ta[++cnt]=t[i]*now,ca[cnt]=c[i]*now;
}
for(fint i=1;i<=n;i++)
{
if(p[i]==0)
for(fint j=t[i];j<=tim;j++)
f[j]=max(f[j],f[j-t[i]]+c[i]);
}
for(fint i=1;i<=cnt;i++)
for(fint j=tim;j>=ta[i];j--)
f[j]=max(f[j],f[j-ta[i]]+ca[i]);
cout<<f[tim];
return 0;
}
```
#### [6,琪露诺](https://www.luogu.com.cn/problem/P1725)
**单调队列优化DP问题**!
首先状态转移方程式可以一眼秒:
$f_i=max(∑_{j=i+l}^{i+r}f_j)+a_i$
肯定过不了QAQ。所以我们考虑单调队列优化。
来一发裸的DP代码(60PTS):
```cpp
signed main()
{
int n,l,r;
cin>>n>>l>>r;
for(fint i=0;i<=n;i++)
cin>>a[i];
for(fint i=0;i<=p;i++)
f[i]=-inf;
f[0]=a[0];
for(fint i=0;i<=n;i++)
if(f[i]!=-inf)
for(fint j=i+l;j<=i+r;j++)
f[j]=max(f[j],f[i]+a[j]);
int ans=-inf;
for(fint i=n;i<=n+r;i++)
ans=max(f[i],ans);
cout<<ans;
return 0;
}
```
就这我还WA了半天,后来发现冰冻值可以为负,嘤嘤嘤。。。
我们考虑优化,用一个长度不超过$r-l+1$单调递减的队列储存此时的$f_j,j∈[l,r]$的最大值。然后直接累加即可。
这样我们就阔以AC这道题了QAQ。
代码(单调队列优化DP):
```cpp
for(fint i=l;i<=n;i++)
{
while(!q.empty()&&f[j]>=q.back().val)
q.pop_back();
q.push_back((node){j,f[j]});
while(!q.empty()&&j-q.front.num>=r-l+1)
q.pop_front();
f[i]=q.front().val+a[i];
j++;
}
```
#### [7,切蛋糕](https://www.luogu.com.cn/problem/P1714)
```cpp
signed main()
{
int n,k;
n=read();
k=read();
for(fint i=1;i<=n;i++)
a[i]=read();
for(fint i=1;i<=n;i++)
s[i]=s[i-1]+a[i];
int head=1;
int maxxs=-inf;
for(fint i=1;i<=n;i++)
{
while(!q.empty()&&s[q.back()]>=s[i])
q.pop_back();
q.push_back(i);
if(q.front()<i-k)
q.pop_front();
maxxs=max(maxxs,s[i]-s[q.front()]);
}
cout<<maxxs;
return 0;
}
```
#### [8,Mowing the Lawn G](https://www.luogu.com.cn/problem/P2627)
很显然,DP方程式:
$f_i=max(f_{j-1}+s_i-s_j,j∈[i-k,i])$
意味着什么?以点$j$为断点求出$j+1$到i部分的和加上前$j-1$个点的最大值.这样求出的东西一定满足题意!
把括号部分的方程用单调队列维护一下即可。
我们在想一想,是否可以对断点进行枚举呢?
记录now为不选元素的最小值,队列元素不超过i-k个(多选一点总是好的)。得到以下代码:
仿佛直接就不是DP了,相当巧妙鸭!
```cpp
signed main()
{
int n,k;
cin>>n>>k;
int sum=0;
for(fint i=1;i<=n;i++)
cin>>a[i],sum+=a[i];
q.push_front((node){0,0});
for(fint i=1;i<=n+1;i++)
{
while(!q.empty()&&i-k>q.back().num+1)
q.pop_back();
int now=q.back().val+a[i];
while(!q.empty()&&now<q.front().val)
q.pop_front();
q.push_front((node){i,now});
}
cout<<sum-q.back().val;
return 0;
}
```
#### [9,BAN-Bank Notes](https://www.luogu.com.cn/problem/P3423)
这题乍一看可能没有头绪,但仔细一想好像和[货币系统](https://www.luogu.com.cn/problem/P5020)又几分相似。
我们可以设物品件数为n,背包体积为k,每件物品体积为1(1个硬币),每件物品价值为$b_i$,每件物品数量$c_i$
那么,**就将问题转化为了多重背包**。
众所周知,裸的多重背包的时间复杂度是$O(nmk)$,状态转移方程为:
$f_{j}=max(f_{j-w{i}}+v_i)$。放在这道题显然是过不了的。那么我们就需要考虑优化。
**怎么优化**?将一件物品可以选多次转化为多件物品,每件物品只能选一次,这样就压掉了一重循环!
**怎么转化**?使用二进制拆分的原理即可。
背包问题处理完了,我们该研究一下对路径的输出了。这个路径显然不能像图论一样通过记录pre结点输出。那么怎么办呢?**DFS**!
我们在更新的使用用vis数组记录物品件数和选择的数量,然后再DFS过程中递归找到被记录得到路径,记下此时物品种类以及件数。
注意,由于我们此前在二进制拆分时把许多物品给变成别的物品了,所以我们要先记录物品的原归属。
代码:
```cpp
int main()
{
cin>>n;
for(fint i=1;i<=n;i++)
cin>>val[i];
for(fint i=1;i<=n;i++)
cin>>num[i];
int k;
cin>>k;
for(fint i=1;i<=n;i++)
{
for(fint j=1;j<=num[i];j<<=1)
v[++cnt]=j*val[i],w[cnt]=j,jin[cnt]=i,num[i]-=j;
if(num[i])
v[++cnt]=num[i]*val[i],w[cnt]=num[i],jin[cnt]=i,num[i]=0;
}
memset(f,0x3f,sizeof(f));
f[0]=0;
for(fint i=1;i<=cnt;i++)
for(fint j=k;j>=v[i];j--)
if(f[j-v[i]]+w[i]<f[j])
f[j]=f[j-v[i]]+w[i],vis[i][j]=1;
cout<<f[k]<<endl;
dfs(k);
return 0;
}
inline void dfs(int x)
{
if(x==0)
{
for(fint i=1;i<=n;i++)
cout<<ans[i]<<" ";
exit(0);
}
while(!vis[cnt][x]&&cnt)
cnt--;
x-=v[cnt],ans[jin[cnt]]+=w[cnt];
cnt--;
dfs(x);
return ;
}
```
#### 10,挖油
一个未知的$01$序列,其中以中间某个地方为界,左侧全1,右侧全0,每次可以询问下标为$i$位是$1or0$,耗费代价为$a_i$,求最少花费多少代价可确定最靠右1的位置;
状态转移方程:
设区间$[i,j]$查询点为$k$
当$i≦j$
$f_{i,j}=min(max(f_{i,k-1},f_{k+1,j})+a_k)$
满足两个单调性:$f$随着$k$的向后推移而而逐渐变大,$f_{i,j}$随着$j$的向后推移而单调递增。
$f_{i,k-1}$单调递增,$f_{k+1,j}$单调递减,两个函数的交点$k_0$.
用单调队列维护即可QAQ。
逆序枚举$i$,顺序枚举$j$,函数单调递增,所以对于每个$i$开一个单调队列。共$n$个单调队列!