强连通分量与拓扑排序略解
hyfhaha
·
·
个人记录
\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 强连通分量与拓扑排序
拓扑排序
(by 百度百科)
$ \ \ \ \ \ \ $照个人理解,拓扑排序通常是在DAG图中寻找一个适合的解决问题的顺序。
### 如何实现拓扑排序
**方法1:BFS(SPFA优化)**
1、先寻找入度为0的点,把它加入队列。
2、搜寻队列,把队列的点G删去,则如果有点的入度有G点的话,入度- -,当发现又出现入度为0的点时,将该点加入队列。
3、拓扑排序的结果为该队列,在执行删点操作的时候存储在一个数组及可。
**方法2:记忆化搜索**
大多数情况下,并不需要显式的拓扑排序
考虑朴素的回溯算法
若从一个给定的点出发,得到的结果是一样的
因此对于每个点,计算完成后可以把结果保存起来,之后直接返回查表的结果即可
**拓扑排序伪代码(1):**
```cpp
Topological_sort(G){
统计图G中每个点的入度(可计算重边,但不可计算自环),记为degree[i]
初始化queue和result为空的队列,并将所有degree为0的点加入queue
while (!queue.empty()){
u = queue.pop() // 队首
result.push(u)
for e 是u的出边(若上面计算了重边,这里也要算,与上面一致)
v是e的指向的点
degree[v]--
if (degree[v] == 0) queue.push(v)
}
return result
}
```
**拓扑排序伪代码(2):**
```cpp
calculate(u){
if (u 已经搜索过) return table[u]
ans = -inf
for (v 是u的出边指向的点)
ans = max(ans, value[u] + calculate(v))
标记u已经搜索过
table[u] = ans
return ans
}
for (i 是G的所有节点)
result = max(result, calculate(i))
print(result)
```
#### ps:源码在我讲完缩点后一起放出来
## 强连通分量——缩点(有向有环图)
$ \ \ \ \ \ \ $现在给出一个有向有环图,那么这个图不是一个DAG,所以不能在这种图上做拓扑排序或其他有关DAG的操作了。

如果我们单独把1,2,3点提出来,把它们看做一个团。
我们把这样一个“团点”叫做强连通分量(scc, strong connected component)
通常来讲,一组互相能到达的点叫做连通分量
当这个连通分量不能再大时,便是强连通分量
### 求强连通分量
把有向有环图抽象成一颗DFS树。
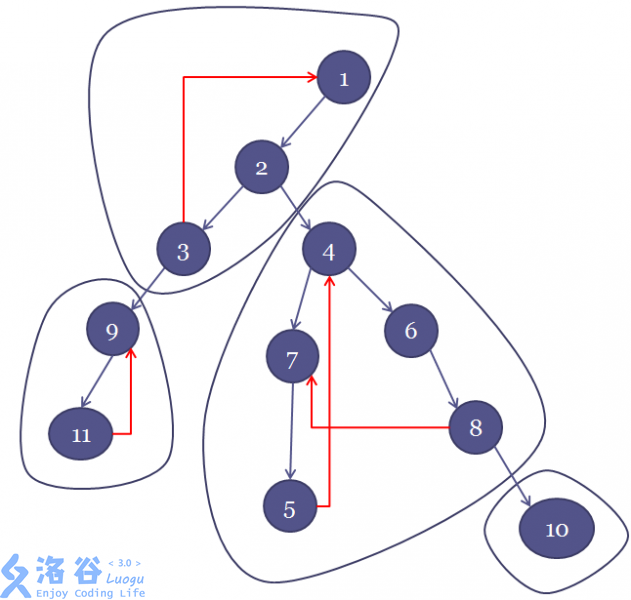
那么每一个图上的圈圈就是一个强连通分量。在DFS树中,强连通分量一定长成这样子。
那么问题就被化简成了确定每个强连通分量的根。
### Tarjan
DFS时我们维护两个数组dfn,low
dfn[i]是i点的进入时间
low[i]是从i点出发,所能访问到的最早的进入时间
#### Tarjan-scc伪码
```cpp
DFS(u)
dfn[u] = low[u] = ++timer
stack.push(u)
state[u]=1 //已访问并入栈
for v 是u的一条出边的端点
if (state[v] == 0) //未访问
DFS(v)
low[u] = min(low[u], low[v])
if (state[v] == 1)
low[u] = min(low[u], dfn[v])
if (dfn[u] == low[u])
stack.pop() until 弹出了u //这些点构成一个强连通分量
弹出的点的state[] = 2
Tarjan_scc(G)
timer = 0
for u 是图G的节点
if (state[u] == 0) DFS(u)
```
那怎么找出一个 强连通分量的所有点
找出scc之后,问题通常会变成两个部分
1、scc内部
2、scc之间,把每个scc看成一个点,则是DAG图
新图怎么连边?
记belong[u]为u所在的scc编号
对于每条边u -> v
若belong[u] != belong[v],则给新图加边 belong[u] -> belong[v]
洛谷【P3387 缩点】
缩点+拓扑排序+DP
代码:
```cpp
#include<bits/stdc++.h>
#define maxn 100001
#define maxm 500001
using namespace std;
struct node{
int to,next,from;
}edge[maxm];
queue <int> q;
vector <int> cb[maxn];
vector <int> rdr[maxn];
int ans[maxn],totq,x,y,v,rd[maxn],u,n,m,sum,vis[maxn],dis_[maxn],dis[maxn];
int dfn[maxn],low[maxn],f[maxn],times,cntqq;
int stack_[maxn],heads[maxm],visit[maxn],cnt,tot,index_;
void add(int x,int y) //建边
{
edge[++cntqq].next=heads[x];
edge[cntqq].from=x;
edge[cntqq].to=y;
heads[x]=cntqq;
return;
}
void tuopu() //拓扑排序
{
for(int i=1;i<=tot;i++) //初始化
{
if(rd[i]==0)
q.push(i); //入度为0的都进队列
}
while(!q.empty())
{
int u=q.front();
q.pop();
ans[++totq]=u;
for(int i=1;i<=cb[u].size();i++)
{
v=cb[u][i-1]; //因为vector是从0开始的,所以减1,下面代码的减1也一样
rd[v]--;
if(rd[v]==0)q.push(v);
}
}
}
void tarjan(int x) //tarjan求强连通分量
{
dfn[x]=low[x]=++times;
stack_[++index_]=x; //手写栈嘿嘿嘿
visit[x]=1;
for(int i=heads[x];i!=-1;i=edge[i].next)
{
if(!dfn[edge[i].to])
{
tarjan(edge[i].to);
low[x]=min(low[x],low[edge[i].to]);
}
else
if(visit[edge[i].to])
low[x]=min(low[x],dfn[edge[i].to]);
}
if(low[x]==dfn[x])
{
tot++;//强连通分量编号
while(1)
{
vis[stack_[index_]]=tot; //index_所在的强连通分量编号,等于前面讲的belong
dis_[tot]+=dis[stack_[index_]]; //强连通分量权值累加
visit[stack_[index_]]=0;index_--;
if(x==stack_[index_+1])break;//手写栈嘿嘿嘿
}
}
}
int main(){
memset(heads,-1,sizeof(heads));
int n,m,x,y;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%d",&dis[i]);
for(int i=1;i<=m;i++){
scanf("%d%d",&x,&y);
add(x,y);
}
for(int i=1;i<=n;i++)if(!dfn[i])tarjan(i); //tarjan
for(int i=1;i<=cntqq;i++){ //拓扑建边
if(vis[edge[i].from]!=vis[edge[i].to])
{
x=vis[edge[i].from];y=vis[edge[i].to];
rd[y]++;cb[x].push_back(y);rdr[y].push_back(x);
}
}
tuopu();
for(int i=1;i<=tot;i++) //dp
{
int w=ans[i];
f[w]=dis_[w];
for(int j=1;j<=rdr[w].size();j++)
f[w]=max(f[w],f[rdr[w][j-1]]+dis_[w]);
}
for(int i=1;i<=tot;i++) //最后统计答案
sum=max(f[i],sum);
printf("%d",sum);
return 0;
}//刚刚好100行
```
## 无向图
$ \ \ \ \ \ \ $现在问题又进一步升级了,有向图变成了无向图,那么完全不可能成为一个DAG了,所以,我们上面讨论的强连通分量等神奇东西在无向图是没有意义的,那么无向图有什么操作呢?
$ \ \ \ \ \ \ $无向图一般讨论**桥**,**割点**,**点双连通分量**或**边双连通分量**
1、若删除一条边后该图不连通,则该边为**桥**
2、若删除一个点后该图不连通,则该点为**割点**
3、无割点的图称是点双连通的,极大的点双连通子图称为**点双连通分量**
4、无桥的图称是边双连通的,极大的边双连通子图称为**边双连通分量**
### 无向图的Tarjan算法
核心仍然是求dfn和low
主体与有向图类似,有两点注意
节点只有两种状态:是否搜索过
要特判是否父亲搜索过来的边
#### 无向图Tarjan伪码
```cpp
DFS(u)
dfn[u] = low[u] = ++timer
vis[u] = true
for v 是u的一条出边(非父边)的端点
if (!vis[v]) //未访问
DFS(v)
low[u] = min(low[u], low[v])
else
low[u] = min(low[u], dfn[v])
Tarjan(G)
timer = 0
for u 是图G的节点
if (!vis[u]) DFS(u)
```
#### 判断割点和桥
**割点**
存在儿子v,low[v] >= dfn[u],则u是割点
根节点特判:若有两个或以上的儿子,则是割点
**桥**
回边不是桥
对于树边,父亲记为u,儿子记为v,若low[v] > dfn[u],则该边是桥
洛谷【P3388 割点】
割点
代码:
```cpp
#include<bits/stdc++.h>
using namespace std;
struct edge{
int next,to;
}e[200010];
int n,m,times,cnt,tot,a,b;
int head[100010],dfn[100010],low[100010];
bool vis[100010];
void add(int x,int y)
{
e[++cnt].next=y;
e[cnt].to=head[x];
head[x]=cnt;
}
void tarjan(int u,int father)
{
dfn[u]=low[u]=++times;
int son=0;
for(int i=head[u];i!=0;i=e[i].to)
{
int v=e[i].next;
if(!dfn[v])
{
tarjan(v,father);
low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u]&&u!=father)
vis[u]=1;
if(u==father)
son++;
}
low[u]=min (low[u],dfn[v]);
}
if(son>=2&&u==father)
vis[u]=1;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
scanf("%d%d",&a,&b);
add(a,b);add(b,a);
}
for(int i=1;i<=n;i++)
if(dfn[i]==0)
tarjan(i,i);
for(int i=1;i<=n;i++)
if(vis[i])
tot++;
printf("%d\n",tot);
for(int i=1;i<=n;i++)
if(vis[i])
printf("%d ",i);
return 0;
}
```
## 后记
我将这两个问题留给大家,如果实在有需要的可以私信我。
question1:如何求点(边)双连通分量
question2:如何记点(边)双连通分量
## 随便给点题
P2341 [HAOI2006]受欢迎的牛
P2002 消息扩散
P1262 间谍网络
POJ 1236
POJ 2186
POJ 2762
POJ 3687
### 以上知识可以优化许多问题,希望大家掌握。
# $ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ $ 谢谢观赏,给个赞呗qwq