我出的（有趣）高考数学题

· · 个人记录

小孩子不懂事出着玩的.jpg

不超纲，无强算。

注解： 此处的难度综合了 思维难度/运算推理的复杂度（按考场时间标准）。部分数据基于同学反馈。

客观题

客观题答案

P1 解答： 答案为 \sqrt{15}。

设四个交点为 A,B,C,D，它们同时满足方程 ① x^2-y^2-1=0， ② x^2-4y=0。

**注解：** 曲线系思想。（本题有其他做法但计算量较大） ------------ **P2 解答：** 答案为 $(0,2]\cup[4,+\infty)$。 假设 $f(x)=x$ 有解，对于 $2^{k-1}\leq x<2^k$，$f(x)=\lambda^kf\big(\frac{x}{2^k}\big)=x$ 展开整理得 $1-\big(\frac{2}{\lambda}\big)^k=\frac{x}{2^{k+1}}\in[\frac{1}{4},\frac{1}{2})$。 记 $t=\frac{2}{\lambda}$，则 $t^k\in(\frac{1}{2},\frac{3}{4}]$。若 $f(x)=x$ 无解，即对于 $k\in N^*$，$t^k$ 都不在 $(\frac{1}{2},\frac{3}{4}]$ 中。 $t\geq 1$ 或 $0<t\leq \frac{1}{2}$ 时显然可行。$t\in (\frac{1}{2},\frac{3}{4}]$ 时不可行，$t\in(\frac{3}{4},1]$ 时步长小于 $\frac{1}{4}$，不能一步跳过限制区域。 综上， $t$ 的范围为 $(0,\frac{1}{2}]\cup[1,+\infty)$，对应 $\lambda$ 范围为 $(0,2]\cup[4,+\infty)$。 **注解：** 按 $2^{k-1}\leq x<2^k$ 分讨后思路是自然的。（但不知为何没啥人会） ------------ **P3 解答：** 答案为 $\rm ABD

正四面体内部最长线段长度为 d，投影后，影子内最长线段不会大于 d ，A 项正确。

正四面体有四个顶点，影子的形状为三角形或（凸）四边形。对于三角形，直径为最长的边，对于四边形，直径为最长的对角线。l 一定时，S 取最大值时是等边三角形或正方形，对应面积为 \frac{\sqrt{3}}{4}d^2 或 \frac{1}{2}d^2（较大），B 项正确。

沿对边中点连线方向投影，影子即为正方形，S=\frac{1}{2}d^2 ，C 项错误。（根据 AB 选项，这也是最大的影子面积）

当 l=d 时，有某条边平行于地面，讨论两个面受光和一个面受光的情况，发现某一面垂直地面时 S 取得最小值，即为 \frac{\sqrt{2}}{4}d^2 ，D 项正确。

注解： 比较考验耐心和空间想象力，慢慢做是不难的。

P4 解答： 答案为 \rm ABD。

记 $g(x)=f(x)-ax-b$，$g''(x)=f''(x)=\frac{2(x-1)}{x^3}$，只有一个零点 $g''(1)=0$。 $g'(x)$ 有2个单调区间，至多 2 零点；$g(x)$ 至多 3 个单调区间，至多 3 零点。由图不难构造 3 个交点，B 正确。 $f(x)$ 没有过 $(0,1)$ 的切线，C 错误。 $f(\frac{1}{x})=\frac{1}{x}-x+2\ln x=-f(x)$。若 $a_1a_n=1$，则 $a_ka_{n-k+1}=1$，$f(a_k)+f(a_{n-k+1})=0$。 高斯求和得 $2\sum_{k=1}^nf(a_k)=\sum_{k=1}^nf(a_k)+f(a_{n-k+1})=0$。 由单调性，$a_na_1<1$ 时，求和小于 $0$，$a_1a_1>1$ 时，求和大于 $0$ ，D 正确。 **注解：** $f(x)+f(\frac{1}{x})=0$ 是经典的构造。 ------------ **P5 解答：** 答案为 $(-\infty,-1)\cup(1,+\infty)$。 由合一公式 $|x\sin x+\cos x|\leq \sqrt{1+x^2}$，故 $|k|>1$ 时无解。 考虑 $x\sin x+\cos x=\pm\sqrt{1+x^2}$ 是否能取等，合一得 $\sin(x+\varphi)=1$（$-1$ 类似） 其中 $\cos \varphi = \frac{x}{\sqrt{x^2}},\sin x=\frac{1}{\sqrt{1+x^2}},\tan \varphi=\frac{1}{x}$。若要取等，$x+\varphi=\frac{\pi}{2}$，取 $\tan$ 得 $\frac{\tan x}{x}=1$，即 $\tan x=x$。 该方程有解，故可取等。由图知 $k\in[-1,1]$ 时原方程有解。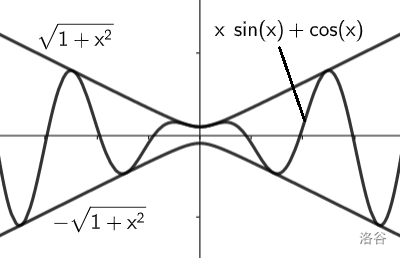 ![](https://cdn.luogu.com.cn/upload/image_hosting/pnsoarin.png) ------------ **P6 解答：** 答案为 $(2,2\sqrt{2})\cup(2\sqrt{2},+\infty)$。 设 $P(x_0,y_0),Q(x_1,y_1),R(x_2,y_2)$，$PA$ 方程为 $y=kx+1$，$k=\frac{y_0-1}{x_0}$。 $PA$ 与 $x^2-y^2=1$ 联立得 $(k^2-1)x^2-2kx+2=0$，$x_0x_1=\frac{2}{k^2-1}$。 代入 $k$ 整理得 $x_1=\frac{2x_0}{y_0^2-x_0^2-2y_0+1}=-\frac{x_0}{y_0}$ （其中 $x_0^2-y_0^2=1$） 代入 $PA$ 整理得 $y_1=\frac{1}{y_0}$，即 $Q\big(-\frac{x_0}{y_0},\frac{1}{y_0}\big)$。由对称性 $R\big(\frac{x_1}{y_1},\frac{1}{y_1}\big)$，代入整理得 $R(-x_0,y_0)$。 $P,R$ 关于 $y$ 轴对称。由 $\Delta=8-4k^2>0$ 排除相切， $k\neq 1$ 排除顶点，最终取值范围为 $(2,2\sqrt{2})\cup(2\sqrt{2},+\infty)$。 **注解：** 难以直接化简 $|PR|$ 的表达式，需发现 $P,R$ 对称的性质。 ------------ **P7 解答：** 答案为 $[-\frac{1}{12},4]$。 令 $x=u+v,y=u-v\ (u,v\in R)$，则 $x^2+y^2-xy=1$ 代入整理得 $u^2+3v^2=1$。 $x^2+y^2+x+y=2u^2+2v^2+2u$，代入消去 $v^2$ 得 $2(\frac{2}{3}u^2+u+\frac{1}{3})$。 其中 $u\in[-1,1]$，易得取值范围为 $[-\frac{1}{12},4]$。（最小值的取等条件是 $x+y=-\frac{1}{6}$，而不是 $x=y$ 或 $x=-y$ 的对称位置） **注解：** 对于轮换对称式，用 $x=u+v,y=u-v$ 换元，得到关于 $v$ 的偶函数，无 $v,uv$ 项，可消去孤立的 $v^2$。 ------------ **P8 解答：** 答案为（1）$[\sqrt{3+\ln 2},+\infty)$ （2）$[2\sqrt{e},+\infty)$。 设 $s=a+b,t=ab$，$s,t$ 能对应回一组 $a,b$ 当且仅当 $s^2-4t\geq 0$ （基本不等式）。 （1）条件即 $\ln t+s^2-2t\geq 2$，$s^2\geq 2t-\ln t+2$，又 $s^2\geq 4t$。 观察图像知，$s^2$ 最小值为 $3+\ln 2$，$a+b$ 范围为 $[\sqrt{3+\ln 2},+\infty)$。 （2）条件即 $8\ln t+s^2-2t\geq 8+2e$，$s^2\geq 2t-8\ln t+8+2e$，又 $s^2\geq 4t$。 观察图像知，$s^2$ 最小值为 $4e$，$a+b$ 范围为 $[2\sqrt{e},+\infty)$。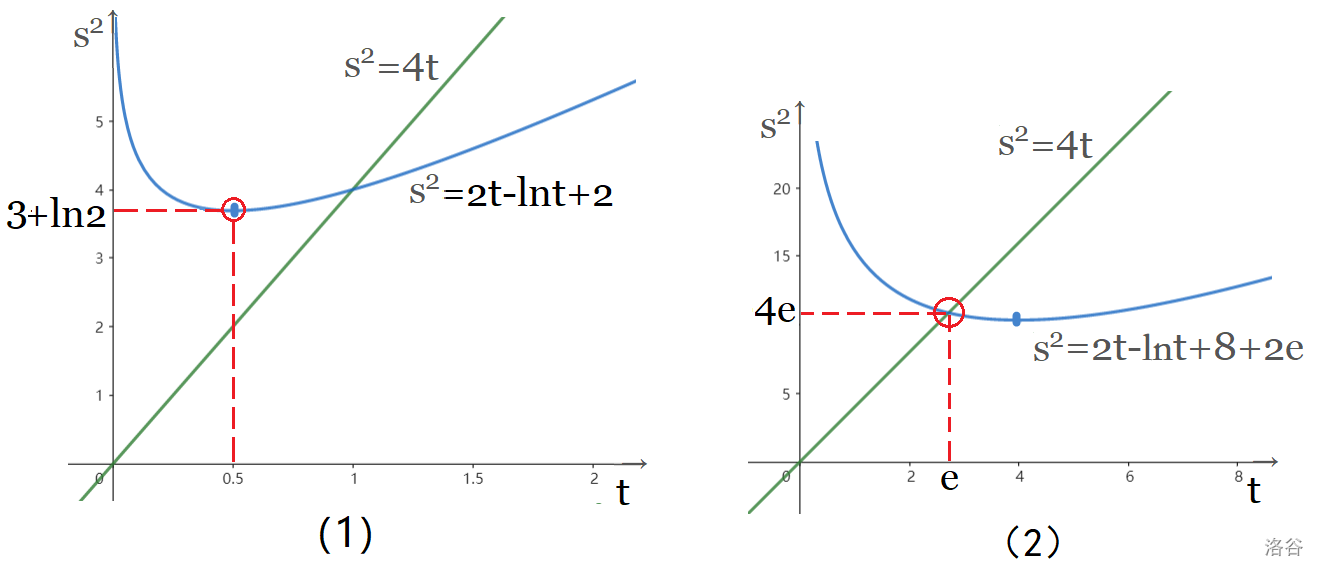 ![](https://cdn.luogu.com.cn/upload/image_hosting/299nb56c.png) **注解：** 根据原式的形式，不难想到把 $a+b,ab$ 换元，但这种换元不是双射。（大多数人用基本不等式做，由于思维不严谨很难拿全分） ------------ **P9 解答：** 答案为 $\big[\frac{5\sqrt{3}}{6},+\infty\big)$。 先解决一个子问题，$|\vec A+\vec c|=|\vec B+\vec c|$，求 $|\vec c|$ 的取值范围（用 $\vec A,\vec B$ 表示）。 平方得 $\vec A^2+2\vec A\cdot\vec c+\vec c^2=\vec B^2+2\vec B\cdot\vec c+\vec c^2$，即 $2(\vec A-\vec B)\cdot\vec c=|\vec B|^2-|\vec A|^2$。 记 $\cos \theta=\cos<\vec A-\vec B,\vec c>$，则 $2|\vec A-\vec B||\vec c|\cos\theta=|\vec B|^2-|\vec A|^2$， $|\vec c|=\dfrac{|\vec B|^2-|\vec A|^2}{2|\vec A-\vec B|\cos\theta}$。 由 $\cos \theta\in[-1,1]$，易知 $|\vec c|$ 最小值为 $\dfrac{\Big||\vec B|^2-|\vec A|^2\Big|}{2|\vec A-\vec B|}$，最大值为 $+\infty$。 依题意取 $\vec A=\vec a+\vec b,\ \vec B=\vec a$，$\dfrac{\Big||\vec B|^2-|\vec A|^2\Big|}{2|\vec A-\vec B|}=\dfrac{\Big||\vec b|^2+2\vec a\cdot \vec b\Big|}{2|\vec b|}=\dfrac{\Big|3+2\vec a\cdot \vec b\Big|}{2\sqrt{3}}\geq \frac{5\sqrt{3}}{6}$，即为最小值。 **注解：** 也存在不错的几何法。 ------------ **P10 解答：** 答案为 $\rm ACD$。 记 $f(b)=be^a+a\ln b$，显然 $f(b)$ 单调递增。 A 选项：$ab<1\ \Leftrightarrow\ b<\frac{1}{a}\ \Leftrightarrow\ 2=f(b)<f(\frac{1}{a})\ \Leftrightarrow\ \frac{e^a}{a}-a\ln a>2\ \Leftrightarrow\ \frac{e^a}{a^2}+\ln a-\frac{2}{a}>0$。 设 $g(a)=\dfrac{e^a}{a^2}-\ln a-\dfrac{2}{a}$，$g'(a)=\dfrac{(a-2)(e^a-a)}{a^3}$，由 $e^a>a$ 易知 $g(a)$ 在 $(0,2)$ 递减，在 $(2,+\infty)$ 递增。 则 $g(a)\geq g(2)=\frac{e^2}{4}-\ln 2-1>0$ ，A 正确。 B 选项：$a$ 趋近于 $0$ 时 $b$ 趋近于 $2$ ，B 错误。 C 选项：$a+\ln b>2-2\ln 2\ \Leftrightarrow\ b>\frac{e^{2-a}}{4}\ \Leftrightarrow\ 2=f(b)>f(\frac{e^{2-a}}{4})\ \Leftrightarrow\ \frac{e^2}{4}-a(2-2\ln 2-a)<2$。 $\frac{e^2}{4}-a(2-2\ln 2-a)$ 最大值为 $\frac{e^2}{4}+(1-\ln 2)^2<2$ ，C 正确。 D 选项：由 C 知 $be^a>\frac{e^2}{4}$，则 $b+e^a\geq 2\sqrt{be^a}>e$。D 正确。 # 解答题 - **P1** $f(x)=ax-\frac{\ln a}{x}-\ln x,\ (a>0)$。 （1）记 $h(a)=f(e^{a-1})$，求 $h(a)$ 的最小值。 （2）存在 $a$ 使 $f(x)\geq b$ 对于 $x\in R$ 恒成立，求 $b$ 的取值范围。 【难度：4.5】 - **P2** $\Delta ABC$ 中，$A=2B$。 （1）求 $\sin C(1+\frac{b^2}{c^2}-\frac{a^2}{c^2})$ 的取值范围。 （2）若 $C$ 为锐角，且 $\dfrac{ab-\cos C}{a-b\cos B}=\dfrac{c}{b}$，求 $b$ 的可能取值。 【难度：5】 - **P3** 在数列 $\{a_n\}$ 中，记前 $n$ 项和为 $S_n$，$a_3=3$，$4S_n=(n+1)(a_n+n)\ (n\in N^*)$。 （1）求 $\{a_n\}$ 的通项公式。 （2）数列 ${b_n}$ 满足 $b_n=\dfrac{1}{a_n\sqrt{a_n}}$。$b_1+b_2+...+b_n<m$ 对 $n\in N^*$ 恒成立，求正整数 $m$ 的最小值。 【难度：5】 - **P4** 抛物线 $\Gamma:x^2=2py(p>0)$，点 $A(0,1)$ 到 $\Gamma$ 的最短距离为 $\frac{\sqrt{3}}{2}$。 （1）求 $\Gamma$ 的标准方程。 （2）$A,B$ 为 $\Gamma$ 上两动点，以 $AB$ 为直径作圆交 $\Gamma$ 于另两点 $C,D$。证明：存在点 $A$ 使得对于所有点 $B$，直线 $CD$ 在 $x$ 轴上截距为定值。 【难度：3.5】 - **P5** 椭圆 $\Gamma:\frac{x^2}{4}+y^2=1$，$A(-1,0),B(1,0)$，过 $B$ 的直线与 $\Gamma$ 交于 $P,Q$，与 $y$ 轴交于 $T$。记 $\Delta APQ$ 的外心为 $M$，求 $\overrightarrow{OT}\cdot\overrightarrow{OM}$ 的取值范围。 【难度：5】 - **P6** $f(x)=2\ln x+x^2+ax-2\ (a\geq -4)$。 （1）求证：$f(x)$ 恰有一零点 $x_0$。 （2）若对于任意满足 $0<x_1<x_0<x_2,\ f(x_1)+f(x_2)>0$ 的 $x_1,x_2$，均满足 $x_1+x_2>2x_0$，求 $a$ 的取值范围。 【难度：4】 - **P7** $f(x)=(2x-1)3^x-a(2x+1)$ 恰有两零点 $x_1,x_2$。 （1）求 $a$ 的取值范围。（2）求 $|x_1-x_2|$ 的最小值。 【难度：5】 - **P8** $k\!\in\!(0,1],\ f(x)=k(\ln x-x+1)+2(x-1)$，$|f(x)|=a$ 有两个解 $x_1,x_2\ (x_1\neq x_2)$ ，求证 $|x_1-x_2|<a$ 。 【难度：5.5】 - **P9** 已知圆 ${\mathcal C}:x^2+y^2=5$ ，抛物线 ${\mathcal E}:y^2=2qx$ ，直线 $l$ 与圆相切于点 $A(1,2)$ 。${\mathcal E}$ 与 $l$ 交于点 $P,Q$ ，过 $P$ 作 ${\mathcal C}$ 的（除 $l$ 外的）另一条切线 $l_1$ ，过 $Q$ 作 ${\mathcal C}$ 的另一条切线 $l_2$ ，$l_1,l_2$ 交于点 $M$ 。求证：$M$ 在定直线上。 【难度：5】 - **P10** 存在 $a\geq b>0$ 使 $(x-b)\ln x-a(x-e-1)\geq c$ 在 $x>0$ 时恒成立，求 $c$ 的取值范围。 【难度：5.5】 ------------ ## 解答题答案 **P1 解答：** （1）$h(a)=ae^{a-1}-e^{1-a}\ln a-a+1$，注意到 $h(1)=1$，下证 $h(a)\geq 1$。 由 $e^{a-1}\geq a,\ \ln a\leq a-1$，$h(a)\geq a^2-e^{1-a}(a-1)-a+1=(a-1)(a-e^{1-a})+1$。 $0<a<1$ 时 $e^{1-a}>1>a$，$a>1$ 时 $e^{1-a}<1<a$，故 $h(a)\geq 1$，则 $h(a)$ 的最小值是 $1$。 （2）① $b\leq 1$。 取 $a=1$，$f(x)=x-\ln x\geq 1\geq b$，符合题意。 ② $b>1$。$f(\frac{1}{a})=1+(1-a)\ln a\leq 1$，与 $f(\frac{1}{a})\geq b$ 矛盾。不存在符合题意的 $a$。 综上所述，$b$ 的取值范围为 $(-\infty,1]$。 **注解：** 过程很短，但猜的成分很大。通过 $x,a$ 上的导数，可以用鞍点法预谋（2）分类的标准（$b$ 的范围以及 $b$ 最大时 $a$ 的取值） ------------ **P2 解答：** （1）记原式为 $P$，$P=\sin C\frac{c^2+b^2-a^2}{c^2}$。 由正弦定理 $P=\sin B\frac{c^2+b^2-a^2}{bc}$，由余弦定理 $P=2\sin B\cos A$。 由 $A=2B$， $P=2\sin B(1-2\sin^2B)=-4\sin^3B+2\sin B$。设 $f(t)=-4t^3+2t$，$f'(t)=-12t^2+2$。 由 $A=2B,\ A+B+C=\pi,\ A,B,C>0$ 得 $B\in(0,\frac{\pi}{3})$，$\sin B\in(0,\frac{\sqrt{3}}{2})$。 $t\in(0,\frac{\sqrt{6}}{6})$ 时，$f'(t)>0$，$f(t)$ 单调递增；$t\in(\frac{\sqrt{6}}{6},+\infty)$ 时，$f'(t)<0$，$f(t)$ 单调递减； $f\big(\frac{\sqrt{6}}{6}\big)=\frac{2\sqrt{6}}{9},\ f(0)=0,\ f(\frac{\sqrt{3}}{2})=-\frac{\sqrt{3}}{2}$。$P$ 取值范围为 $\big(-\frac{\sqrt{3}}{2},\frac{2\sqrt{6}}{9}]$。 （2） （解法一）试证 ① $\frac{a-b\cos C}{a-b\cos B}=\frac{c}{b}$，由正弦定理即 $\frac{\sin A-\sin B\cos C}{\sin A-\sin B\cos B}=\frac{\sin C}{\sin B}$。 由 $A+B+C=\pi$，$\sin A=\sin(B+C)$，$\sin A-\sin B\cos C=\sin C\cos B$。由 $C\in(0,\pi),\sin C>0$，整理得 $\frac{\cos B}{\sin A-\sin B\cos B}=\frac{1}{\sin B}$ 即 $\sin A=2\sin B\cos B=\sin 2B$，由 $A=2B$，① 式成立。 于是 $\frac{ab-\cos C}{a-b\cos B}=\frac{c}{b}=\frac{a-b\cos C}{a-b\cos B}$ 则 $ab-\cos C=a-b\cos C$ 即 $(b-1)(a+\cos C)=0$。 由 $C\in(0,\frac{\pi}{2})$，可知 $\cos C>0$，故 $b=1$。 （解法二）代入余弦定理化简得 ① $b^3-bc^2+b^2-c^2+a^2(2c-3b+1)=0$。 由 $A=2B$，$\sin A=\sin 2B=2\sin B\cos B$，由正弦定理 $a=2b\cos B$，代入余弦定理整理得 $(b-c)(a^2-b^2-bc)=0$。 $b\neq c$ 时 $a^2=b^2+bc$；$b=c$ 时经验证也满足。 在 ① 中代入消去 $a^2$ 整理得 $(b-1)(2b^2+bc-c^2)=0$。 由 $C\in (0,\frac{\pi}{2})$ 知 $a^2+b^2>c^2$，代入消去 $a^2$ 得 $2b^2+bc-c^2>0$，故 $b=1$。 **注解：** 取 $A=\frac{\pi}{2},B=\frac{\pi}{4}$ 猜出 $b=1$。解法一中配凑成齐次式再证明，解法二中可以预判到因式 $(b-1)$。 ------------ **P3 解答：** （1）① $4S_n=(n+1)(a_n+n)$，② $4S_{n+1}=(n+2)(a_n+n+1)$，② $-$ ① 整理得 $(n+1)a_n=(n-2)a_{n+1}+2(n+1)\ \Rightarrow\ (n+1)(a_n-n)=(n-2)(a_{n+1}-n-1)$。 $n\geq 3$ 时 $a_{n+1}-n-1=\frac{n+1}{n-2}(a_n-n)$。记 $b_n=\frac{n+1}{n-2}>0

由 a_3=3，n\geq 4 时 a_n-n=b_{n-1}b_{n-2}...b_{3}(a_3-3)=0，故 a_n=n。

① 中令 n=1 得 4S_1=2(a_1+1)\ \Rightarrow\ a_1=1。令 n=2 得 4S_2=3(a_2+2)\ \Rightarrow\ a_2=2。也符合 a_n=n。

综上，\{a_n\} 的通项公式为 a_n=n。

（2）设 T_n=\sum\limits_{k=1}^nb_k，T_n<m 恒成立。

n>1$ 时 $b_n=\frac{1}{n\sqrt{n}}\geq\frac{2}{n(\sqrt{n}+\sqrt{n-1})}=\frac{2(\sqrt{n}-\sqrt{n-1})}{n}\geq \frac{2(\sqrt{n}-\sqrt{n-1})}{\sqrt{n(n-1)}}=2\big(\frac{1}{\sqrt{n-1}}-\frac{1}{\sqrt{n}}\big) $b_n=\frac{1}{a_n\sqrt{a_n}}=\frac{1}{n\sqrt{n}}\geq\frac{2}{n(\sqrt{n}+\sqrt{n+1})}=\frac{2(\sqrt{n+1}-\sqrt{n})}{n}\geq \frac{2(\sqrt{n+1}-\sqrt{n})}{\sqrt{n(n+1)}}=2\big(\frac{1}{\sqrt{n}}-\frac{1}{\sqrt{n+1}}\big) T_n\geq b_1+2(\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{3}}+\frac{1}{\sqrt{3}}-\frac{1}{\sqrt{4}}+...+\frac{1}{\sqrt{n}}-\frac{1}{\sqrt{n+1}})=1+\sqrt{2}-\frac{1}{\sqrt{n+1}} **注解：** 某些地区这类技巧教得比较多，难度可能要降一档。 ------------ **P4 解答：** （1）设 $\Gamma$ 上一点为 $P\big(x_0,\frac{x_0^2}{2p}\big)$，$|AP|^2=x_0^2+\big(\frac{x_0^2}{2p}-1\big)^2=\frac{t^2}{2p}+\frac{p-1}{p}t+1$ （其中 $t=x_0^2\geq 0$） 其对称轴为 $t=1-p$。若 $p>1$，其最小值在 $t=0$ 时取得 $1$，舍去。 若 $0<p\leq 1$，其最小值在 $t=1-p$ 时取得 $1-\frac{(p-1)^2}{2p}=\big(\frac{\sqrt{3}}{2}\big)^2$，解得 $p=\frac{1}{2}$ 或 $2$（舍去） $\Gamma$ 方程为 $y=x^2$。 （2）设 $A(x_1,x_1^2),B(x_2,x_2^2),C(x_3,x_3^2),D(x_4,x_4^2)$。 $k_{AC}=\frac{x_1^2-x_3^2}{x_1-x_3}=x_1+x_3$，同理 $k_{BC}=x_1+x_3$。 由 $A,B,C,D$ 四点共圆，$AB$ 为直径，$AC\perp BC,\ AD\perp BD$。 $k_{AC}k_{BC}=-1$ 代入整理得 $x_3^2+(x_1+x_2)x_3+x_1x_2+1=0$，对 $x_4$ 同理。 $C,D$ 同时满足方程 $y+(x_1+x_2)x+x_1x_2+1=0$，其即为 $CD$ 方程。 令 $y=0$ 得截距 $d=-\frac{x_1x_2+1}{x_1+x_2}$ 对所有 $x_2$ 为定值，则 $\frac{1}{x_1}=\frac{x_1}{1}$，解得 $x_1=\pm 1$。 $A(1,1)$ 时 $d=-1$，或 $A(-1,1)$ 时 $d=1$。 **注解：** 本题解法很多，做出来不难，但简洁的做法可以节省大量时间。 ------------ **P5 解答：** 设 $PQ$ 方程为 $x=my+1$ （由题知 $PQ$ 不为 $y=0$，$m$ 存在），令 $x=0$ 得 $y_T=-\frac{1}{m}$。（$m\neq 0$） $P,Q$ 符合椭圆 $\Gamma$ 方程 ① $x^2+4y^2-4=0$ 与 $PQ$ 方程 ② $x-my-1=0$。 ① $-\frac{3}{2}$ ② 得 ③ $x^2+4y^2-\frac{3}{2}x+\frac{3}{2}my-\frac{5}{2}=0$，代入知 $A(-1,0)$ 符合 ③。 $A(-1,0)$ 在直线 $x+my+1=0$ 上，$P,Q,A$ 符合 ④ $(x-my-1)(x+my+1)=0$。 $P,Q,A$ 符合 $\frac{m^2+1}{m^2+4}$ ③ $+\frac{3}{m^2+4}$ ④ 即 $x^2+y^2-\frac{3m^2+3}{2m^2+8}x+m\frac{3m^2-9}{2m^2+8}y-\frac{5m^2+11}{2m^2+8}=0$。 （或书写：其 $x^2,y^2$ 系数为 $1$，$xy$ 系数为 $0$，$y$ 系数为 $\dots$【此处 $x$ 系数和常数项不需要】） 其即为 $\Delta APQ$ 外接圆的标准方程。则 $y_M=-\frac{3m(m^2-3)}{4(m^2+4)}$。 $\overrightarrow{OT}\cdot\overrightarrow{OM}=y_Ty_M=\frac{-21}{4m^2+16}+\frac{3}{4}$，$m^2\in(0,+\infty)$，其取值范围为 $\Big(-\frac{9}{16},\frac{3}{4}\Big)$。 **注解：** 利用曲线系思想得到外接圆方程，其中构造了一条斜率相反的直线。 ------------ **P6 解答：** （1）$f(x)$ 定义域 $(0,+\infty)$。$f'(x)=\frac{2}{x}+2x+a\geq 2\sqrt{\frac{2}{x}\cdot 2x}+a=4+a\geq 0, f(x)$ 单调递增。 $x>0,x\to 0,\ f(x)\to-\infty$；$x\to+\infty,\ f(x)\to+\infty$，则 $f(x)$ 恰有一零点 $x_0$。 （2）设 $F(x)=f(x)+f(2x_0-x),\ F'(x)=f'(x)-f'(2x_0-x)=4(x-x_0)\Big(1-\frac{1}{x(2x_0-x)}\Big)

① a\geq 1，则 f(1)\geq 0=f(x_0),\ x_0\leq 1

由 x(2x_0-x)\leq x_0^2 则 1-\dfrac{1}{x(2x_0-x)}\leq 0。x\!\in\!(0,x_0) 时 F'(x)>0,\ F(x) 单调递增，F(x_1)<F(1)=0

即 f(x_1)+f(2x_0-x_1)<0，与 f(x_1)+f(x_2)>0 相加整理得 f(2x_0-x_1)<f(x_2)，由 f(x) 单调递增，2x_0-x_1<x_2 则 x_1+x_2>2x_0，符合题意。

② -4\leq a<1，则 f(1)<0=f(x_0),\ x_0>1.

$1<x_1<x_0$ 时，$F(x_1)>F(x_0)=0$ 即 $f(x_1)+f(2x_0-x_1)>0$，取 $x_2=2x_0-x_1$，满足 $f(x_1)+f(x_2)>0$ 但 $x_1+x_2=2x_0$，舍去。 综上，$a$ 的取值范围为 $[1,+\infty)

注解： 拐点偏移，构造函数法需证（x\!\in\!(0,x_0) 时）F(x)=f(x)+f(2x_0-x)<0，端点值 F(x_0)=2f(x_0)=0, 再证 F'(x)=f'(x)-f'(2x_0-x)>0 ，端点值 F'(x_0)=0 ，需 F''(x_0)=2f''(x_0)>0 ，可得 0<x_0\leq 1。（端点效应）

P7 解答：

不妨设 x_1<x_2。

（1）设 g(x)=\frac{2x-1}{2x+1}3^x\ (x\neq -\frac{1}{2})。易知 f(-\frac{1}{2})\neq 0，f(x) 的零点与 g(x)=a 的解相同。

① $a\leq 0$。$x<-\frac{1}{2}$ 时 $g(x)>0$，$g(x)=a$ 无解。$x>-\frac{1}{2}$ 时至多一解，舍去。 ② $a> 0$。$x\rightarrow -\infty,g(x)\rightarrow 0$；$x<-\frac{1}{2},x\rightarrow -\frac{1}{2},g(x)\rightarrow +\infty$ 。故恰存在 $x_1\!\in\!(-\infty,-\frac{1}{2}),g(x_1)=a$。 $g(\frac{1}{2})=0$；$x\rightarrow +\infty,g(x)\rightarrow +\infty$ 。故恰存在 $x_2\!\in\!(\frac{1}{2},\infty),g(x_2)=a$。故 $g(x)=a$ 恰有两解。 综上，$a$ 的取值范围为 $(0,+\infty)$ 。 （2）设 $p(x)=\ln g(x)=(\ln3)x+\ln\frac{2x-1}{2x+1}\ \ \big(x\!\in\!(-\infty,-\frac{1}{2})\cup(\frac{1}{2},+\infty)\big)$ 。 由 $f(x)$ 的单调性，$p(x)$ 在 $(-\infty,-\frac{1}{2}),(\frac{1}{2},+\infty)$ 分别单调递增。 $p(-x)=-(\ln3)x+\ln\frac{-2x-1}{1-2x}=-p(x)$ ，故 $p(x)$ 为奇函数。 由 (1) 知 $a>0$ ，则 $g(x)=a$ 与 $p(x)=\ln a$ 同解。 $a=1$ 时解 $p(x)=\ln a=0$ 易得 $x_1=-1,x_2=1,|x_1-x_2|=2$ 。 另一方面，设 $h(x)=(\frac{4}{3}+\ln3)(x-1)-p(x),\ h'(x)=\frac{(x-1)(\frac{16}{3}x+4)}{(2x-1)(2x+1)}$ 。 $x\!\in\!(\frac{1}{2},1),\ h'(x)<0,\ h(x)$ 单调递减；$x\!\in\!(1,+\infty),\ h'(x)>0,\ h(x)$ 单调递增。 $x>\frac{1}{2}$ 时，$h(x)\geq h(1)=0$，即 $p(x)\leq (\frac{4}{3}+\ln3)(x-1)$。 由 $p(x)$ 为奇函数，以 $-x$ 代 $x$ 得 $x<-\frac{1}{2}$ 时 $p(x)\geq (\frac{4}{3}+\ln3)(x+1)$。 则 $(\frac{4}{3}+\ln3)(x_2-1)-(\frac{4}{3}+\ln3)(x_1+1)\geq p(x_2)-p(x_1)=0$ ，则 $x_2-x_1\geq 2$ 。 综上，$|x_2-x_1|$ 的最小值为 $2$ 。 **注解：** $f(x)f(-x)=1,f(x)+f(\frac{1}{x})=0$ 等经典构造都可以通过指对换元变为奇函数/偶函数。利用对称性进行切线放缩，可以大大简化计算。 ------------ **P8 解答：** 引理（易证）：$0<x<1$ 时 $\ln x<2\frac{x-1}{x+1}$， $x>1$ 时 $\ln x>2\frac{x-1}{x+1}$。 $f(x)$ 定义域 $(0,+\infty)$ 。$f(x)=k\ln x+(2-k)x+k-2$ ，由 $k\!\in\!(0,1]$ ，$f(x)$ 单调递增。 $|f(x)|=a\ \Longleftrightarrow\ f(x)=\pm a\ (a\geq 0)$ ，不妨设 $x_1<x_2$，由 $f(x)$ 单调递增，$f(x_1)=-a,f(x_2)=a$。 由 $x_1\neq x_2$ ，$a>0$ ，又 $f(1)=0$ ，则 $0<x_1<1<x_2$ 。 设 $h(x)=k\Big(2\frac{x-1}{x+1}-x+1\Big)+2(x-1)=(2-k)x-\frac{4k}{x+1}+3k-2$ 。由 $k\!\in\!(0,1]$ ，$h(x)$ 单调递增。 $x>-1,x\rightarrow -1,h(x)\rightarrow -\infty$；$x\rightarrow +\infty,h(x)\rightarrow +\infty$ 。故 $h(x)$ 在 $(-1,+\infty)$ 上取值范围为 $\bf R$。 取 $t_1,t_2>-1$ 满足 $h(t_1)=f(x_1)=-a,\ h(t_2)=f(x_2)=a$ 。 根据引理，$0<x<1$ 时 $h(x)>f(x)$，$x>1$ 时 $h(x)<f(x)$。 则 $h(x_1)>f(x_1)=h(t_1),h(x_2)<f(x_2)=h(t_2)\ \Longrightarrow\ x_1>t_1,x_2<t_2\ \Longrightarrow\ x_2-x_1<t_2-t_1$ 。 记 $p(x)=h(x-1)\ ,w_1=t_1+1,w_2=t_2+1$ ，则 $p(w_1)=h(t_1+1-1)=h(t_1)=-a,\ p(w_2)=a$ 。 代入得 $\begin{cases}(2-k)w_1-4k/w_1+4(k-1)=-a\\(2-k)w_2-4k/w_2+4(k-1)=a\end{cases}$ ，两式相减得 $\Big(2-k+\frac{4k}{w_1w_2}\Big)(w_2-w_1)=2a$ (*)。 $p(x)+p(\frac{4}{x})=2(1-k)\big(x+\frac{4}{x}-4\big)$ ，由 $k\!\in\!(0,1]$ 且 $x+\frac{4}{x}\geq 2\sqrt{x\cdot\frac{4}{x}}=4,\ p(x)+p(\frac{4}{x})\geq 0$ 。 则 $p(w_1)+p(\frac{4}{w_1})\geq 0$ 即 $p(\frac{4}{w_1})\geq -p(w_1)=p(w_2)$ ，由 $p(x)$ 单调递增，$\frac{4}{w_1}\geq w_2$ 即 $w_1w_2\leq 4$ 。 结合 (*) 式，$2a\geq \Big(2-k+\dfrac{4k}{4}\Big)(w_2-w_1)=2(w_2-w_1)$ ，则 $x_2-x_1<t_2-t_1=w_2-w_1\leq a$ 。 **注解：** 起手用飘带拟合，比较逆天。后面都是对简单分式的处理。 ------------ **P9 解答：** 记原点 $O(0,0)$ ，由 $l$ 与 $\mathcal C$ 切于点 $A$ ，$OA\perp l$ ，则 $ k_l=-\frac{1}{ k_{OA}}=\frac{1}{2}$ 。可得 $l$ 方程为 $x+2y=5$ 。 以 $(5,0)$ 为原点，相同坐标轴方向建立新坐标系。在新坐标系中： $$l:x+2y=0\qquad\mathcal C:(x+5)^2+y^2=5\qquad\mathcal E:y^2=2p(x+5)$$ $\begin{cases}y^2=2p(x+5)\\x+2y=0\end{cases}$得 $y^2+4py-10p=0$ 。 设 $P(-2y_1,y_1),Q(-2y_2,y_2)$ ，则 $\frac{y_1+y_2}{y_1y_2}=\frac{-4p}{-10p}=\frac{2}{5}$。 设 $M(x_0,y_0)$ ，$MP$ 方程 $(y-y_0)(x_0+2y_1)=(y_0-y_1)(x-x_0)$ 即 $(x_0+2y_1)y+(y_1-y_0)x-(2y_0y_1+x_0y_1)=0

由 MP 与圆 \mathcal C 相切得 \dfrac{|-5(y_1-y_0)-(2y_0y_1+x_0y_1)|}{\sqrt{(x_0+2y_1)^2+(y_1-y_0)^2}}=\sqrt{5} 即 [y_1(2y_0+x_0+5)-5y_0]^2=5[(x_0+2y_1)^2+(y_1-y_0)^2]

即 [(2y_0+x_0+5)^2-25]y_1^2-10(2y_0^2+x_0y_0+4y_0+2x_0)y_1+20y_0^2-5x_0^2=0 。

对于 y_2 同理。可得 y_1,y_2 满足二次方程：

[(2y_0+x_0+5)^2-25]y^2-10(2y_0^2+x_0y_0+4y_0+2x_0)y+20y_0^2-5x_0^2=0 \dfrac{y_1+y_2}{y_1y_2}=\dfrac{10(2y_0^2+x_0y_0+4y_0+2x_0)}{20y_0^2-5x_0^2}=\dfrac{2(2y_0+x_0)(y_0+2)}{(2y_0+x_0)(2y_0-x_0)}=\dfrac{2(y_0+2)}{2y_0-x_0}=\dfrac{2}{5}

可得 x_0=-3y_0-10 ，M 过 x=-3y-10 ，原坐标系中 M 过 x=-3y-5 。

注解： 将原点移动到 l 与 x 轴交点，可消去 l 中常数项，便于后面的因式分解。

P10 解答：

设 k=\frac{a}{b}\in[1,+\infty)，f(x)=x\ln x-b(k\ln x+x-e-1)。

记 g(x)=k\ln x+x-e-1，g(x) 单调递增，g(e)=k-1\geq 0，g(1)=-e<0。g(x) 恰有一零点 x_0\in(1,e]。

设 h(x)=x\ln x，h'(x)=\ln x+1。x>1 时 h'(x)>0，h(x) 单调递增。故 c\leq f(x_0)=h(x_0)\leq h(e)=e。

另一方面，取 a=b=\frac{2e}{e+1}，f'(x)=\ln x+1-\frac{2e}{(e+1)}\big(1+\frac{1}{x}\big)。

此时 $f(x)\geq f(e)=e$，$c$ 可取 $(-\infty,e]$。 综上，$c$ 的范围为 $(-\infty,e]$。 **注解：** 没学过竞赛不等式，也许有高妙做法。