卡特兰数 (Calatan Number)
MiPloRAs_3316
·
·
个人记录
\large{\textbf{\textsf{\color{RoyalBlue}{引例}}}}
下图是 $n=5$ 时的图示。
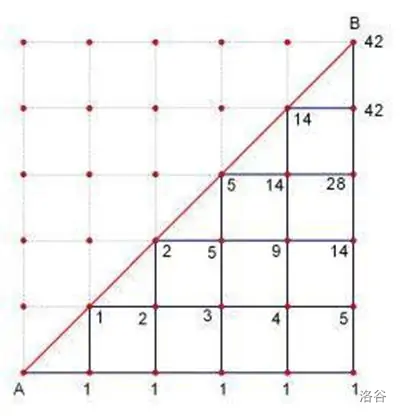
我们将**红线**上的一排数,称作 **卡特兰数(Catalan 数列)**:
| $i$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- |
| $C_i$ | 1 | 1 | 2 | 5 | 14 | 42 | 132 | 429 | 1430 |
---
$\large{\textbf{\textsf{\color{RoyalBlue}{公式}}}}
\textbf{\textsf{\color{#900021}{定义式:}}}
从原点 (0,0) 出发,每次向 x 轴或者 y 轴正方向移动 1 个单位,直到到达 (n,n) 点,且在移动过程中不越过第一象限平分线的移动方案总数。
\sum_{i=1}^{n} H_{i-1} H_{n-i} & n \geq 2, n \in \mathbf{N_{+}}\\
1 & n = 0, 1
\end{cases}
\textbf{\textsf{\color{#900021}{递推公式:}}}
&= \binom{2n}{n} - \binom{2n}{n-1}
\end{aligned}
\textbf{\textsf{\color{#900021}{递推公式:}}}
H_n = \frac{4n-2}{n+1}H_{n-1}
证明:
&= \frac{1}{n+1}\cdot \frac{(2n)!}{n!\cdot n!}\\
&= \frac{1}{n+1}\cdot \frac{(2n-2)!\cdot (2n-1) \cdot 2n}{(n-1)!\cdot (n-1)!\cdot n^2}\\
&= \frac{1}{n+1}\cdot \frac{(2n-1)\cdot 2n}{n}\cdot \frac{1}{n}\cdot \binom{2n-2}{n-1}\\
&= \frac{4n-2}{n+1}H_{n-1}
\end{aligned}