函数的极限

· · 个人记录

说在前面的话

关于函数极限的定义，大家似乎在刚学高数的时候很困扰，不要担心，只要认真去理解，多花时间反复研读定义，你一定会有所收获，我的这篇文章也会帮助你理解它。这两天收到了大家的反馈，我很高兴你们能支持我，同时细心的你们也给我提出了几处失误，我一一改正了。失误是难免的，以后我尽量规避，同时也请你们发现时及时提出。

如果你已经看了我前面一节关于数列极限（戳我了解）的内容，相信你一定会很容易理解本讲内容，如果你还没有看过，本人也[墙裂...墙裂...]建议你回头看看。多研读几遍，只有这样才能内化为自己的知识。

懂了定义，本讲的其他部分也就迎刃而解了，但是如果你在看本文中的例题时还是有点困难，那么再不厌其烦地回头研读定义吧。我们一起学习吧~

函数极限的定义

1. 自变量 $x$ 任意接近于有限值 $x_0$ 或者说趋近于有限值 $x_0$（记作 $x\to x_0$）时，对应的函数 $f(x)$ 的变化情形； 2. 自变量 $x$ 的绝对值 $|x|$ 无限增大即趋近于无穷大（记作 $x\to\infty$）时，对应的函数值 $f(x)$ 的变化情形。 ## 1. 自变量趋于有限值函数的极限 $\quad$ 现在考虑自变量 $x$ 的变化过程为 $x\to x_0$。如果在 $x\to x_0$ 的过程中，对应的函数值 $f(x)$ 无限接近于确定的数值 $A$，那么就是说 $A$ 是函数 $f(x)$ 当 $x\to x_0$ 时的极限。当然，这里我们首先假定函数 $f(x)$ 在点 $x_0$ 的某个去心邻域（以 $x_0$ 为中心的任何开区间称为点 $x_0$ 的邻域，记作 $U(x_0)$；在 $U(x_0)$中去掉中心 $x_0$ 后，称为点 $x_0$ 的去心邻域）内是有定义的。 $\quad$ 在 $x\to x_0$ 的过程中，对应的函数值 $f(x)$ 无限接近于 $A$，就是 $|f(x)-A|$ 能任意小，如数列极限概念所述，$|f(x)-A|$ 能任意小这件事可以用 $|f(x)-A|<\epsilon$ 来表达，其中 $\epsilon$ 是任意给定的正数。因为函数值 $f(x)$ 无限接近于$A$ 是在 $x\to x_0$ 的过程中实现的，所以对于任意给定的正数 $\epsilon$，只要求充分接近于 $x_0$ 的 $x$所对应的函数值 $f(x)$ 满足不等式 $|f(x)-A|<\epsilon$；而充分满足于 $x_0$ 的 $x$ 克表示为 $0<|x-x_0|<\delta$，其中 $\delta$ 是某个正数。从几何上看，适合不等式 $0<|x-x_0|<\delta$ 的 $x$ 的全体，就是点 $x_0$ 的去心邻域，而邻域半径（设 $x_0\in R,\delta>0$，开区间$(x_0-\delta,x_0+\delta)$ 称为点 $x_0$ 的 $\delta$ 邻域，记作 $U(x_0,\delta)$，点 $x_0$ 的去心邻域记作 $\dot{U}(x_0,\delta)$，$\delta$ 记作邻域半径）$\delta$ 则体现了 $x$ 接近 $x_0$ 的程度。 $\quad$ 通过以上分析，我们给出 $x\to x_0$ 时函数的极限定义如下： $\quad$ **定义$1\quad$ 设函数 $f(x)$ 在点 $x_0$ 的某一去心邻域内有定义。如果存在常数 $A$，对于任意给定的正数 $\epsilon$（无论它多么小），总存在正数 $\delta$，使得当 $x$ 满足不等式 $0<|x-x_0|<\delta$ 时，对应的函数值 $f(x)$ 都满足不等式** $$|f(x)-A|<\epsilon$$ ### 那么常数 $A$ 就叫做函数 $f(x)$ 当 $x\to x_0$ 时的极限，记作 $$\lim\limits_{x\to x_0}f(x)=A \quad or \quad f(x)\to A(x\to x_0)$$ 我们指出，定义中 $0<|x-x_0|$ 表示 $x\ne x_0$，所以 $x\to x_0$ 时 $f(x)$ 有没有极限，与 $f(x）$ 在点 $x_0$ 是否有定义并无关系。 $\quad$ 定义 $1$ 可以简单表示为 $\lim\limits_{x\to x_0}f(x)=A\Leftrightarrow\forall\epsilon>0,\exists\delta>0,$ 当 $0<|x-x_0|<\delta$ 时，有 $|f(x)-A|<\epsilon$。 $\quad$ 函数 $f(x)$ 当 $x\to x_0$ 时的极限为 $A$ 的几何解释如下：任意给定一正数 $\epsilon$,作为平行于 $x$ 轴的两条直线 $y=A+\epsilon$ 和 $y=A-\epsilon$，介于这两条直线之间是一横条区域。根据定义，对于给定的 $\epsilon$，存在着点 $x_0$ 的一个 $\delta$ 邻域 $(x_0-\delta,x_0+\delta)$，当 $y=f(x)$ 的图形上的点的横坐标 $x$ 在邻域 $(x_0+\delta,x_0+\delta)$ 内，但 $x\ne x_0$ 时，这些店的纵坐标 $f(x)$ 满足不等式 $$|f(x)-A|<\epsilon$$ 或 $$A-\epsilon<f(x)<A+\epsilon$$ 亦即这些点落在下图所作的横条区域内。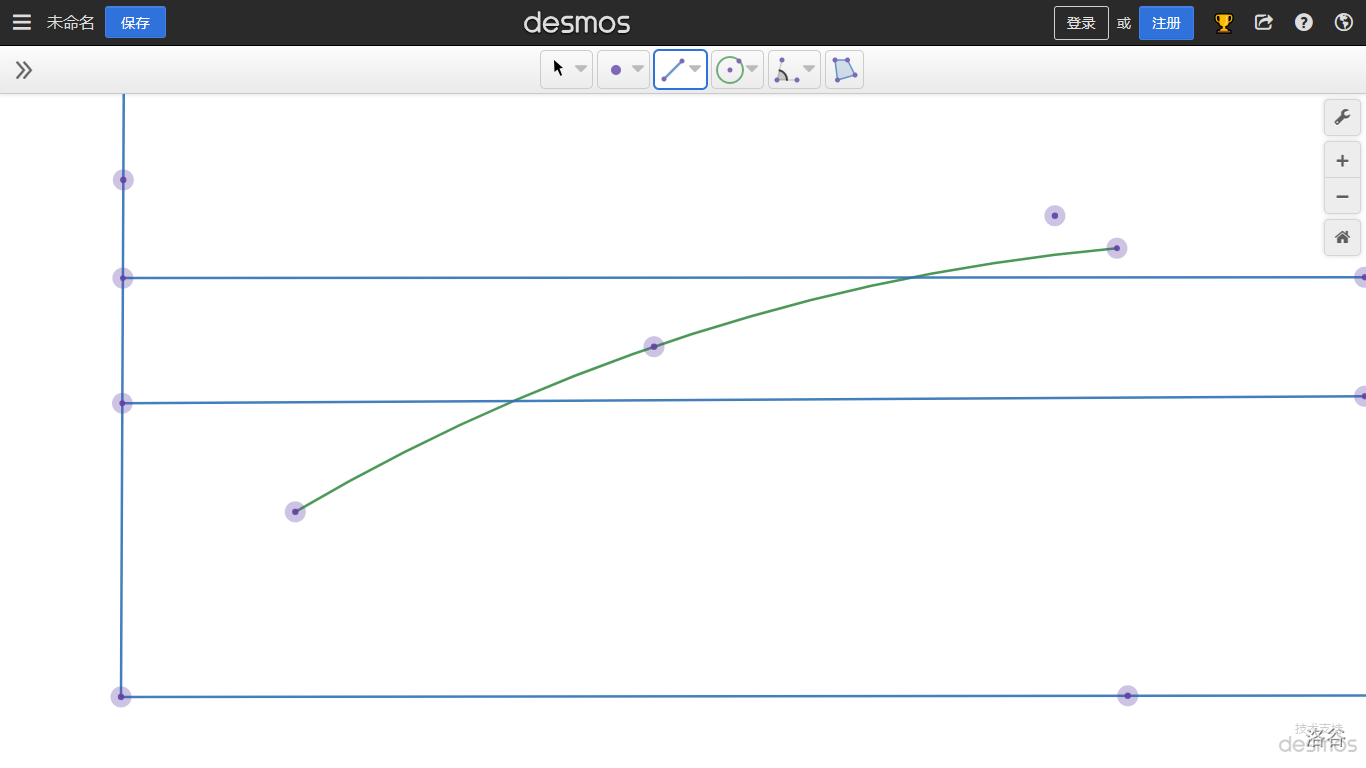![](https://cdn.luogu.com.cn/upload/image_hosting/y039lh7h.png) 例1. 证明 $\lim\limits_{x\to x_0}c=c$，此处 $c$ 为一常数。 证 $\quad$ 这里 $|f(x)-A|=|c-c|=0$，因此 $\forall\epsilon>0$，可任取 $\delta>0$，当 $0<|x-x_0|<\delta$，能使不等式 |$f(x)-A|=|c-c|=0<\epsilon$ 成立。所以 $\lim\limits_{x\to x_0}c=c$。 例2. 证明 $\lim\limits_{x\to x_0}x=x_0$。 证 $\quad$ 这里 $|f(x)-A|=|x-x_0|$，因此 $\forall\epsilon>0$，总可取 $\delta=\epsilon$，当 $0<|x-x_0|<\delta=\epsilon$ 时，能使不等式 $|f(x)-A|=|x-x_0|<\epsilon$ 成立。所以 $\lim\limits_{x\to x_0}x=x_0$。 例3. 证明 $\lim\limits_{x\to 1}(2x-1)=1$。 证 $\quad$ 由于 $$|f(x)-A|=|(2x-1)-1|=2|x-1|,$$ 为了使 $|f(x)-A|<\epsilon$，只要 $$|x-1|<\dfrac{\epsilon}{2}.$$ 所以，$\forall\epsilon>0$，可取 $\delta=\dfrac{\epsilon}{2}$，则当 $x$ 适合不等式 $$0<|x-1|<\delta$$ 时，对应的函数值 $f(x)$ 就满足不等式 $$|f(x)-1|=|(2x-1)-1|<\epsilon$$ 从而 $$\lim\limits_{x\to1}(2x-1)=1.$$ 例4. 证明 $\lim\limits_{x\to1}\dfrac{x^2-1}{x-1}=2$. 证 $\quad$ 这里，函数在点 $x=1$ 是没有定义的，但是函数当 $x\to1$ 时的极限存在或不存在与它并无关系。事实上，$\forall\epsilon>0$，将不等式 $$|\dfrac{x^2-1}{x-1}-2|<\epsilon$$ 约去非零因子 $x-1$ 后，就化为 $$|x+1-2|=|x-1|<\epsilon$$ 因此，只要取 $\delta=\epsilon$ 后，就化为 $$|\dfrac{x^2-1}{x-1}-2|<\epsilon$$ 所以 $$\lim\limits_{x\to1}\dfrac{x^2-1}{x-1}=2.$$ 例5. 证明：当 $x_0>0$ 时，$\lim\limits_{x\to x_0}\sqrt{x}=\sqrt{x_0}$。 证 $\quad\;\forall\epsilon>0$，因为 $$|f(x)-A|=|\sqrt{x} -\sqrt{x_0}|=|\dfrac{x-x_0}{\sqrt{x}+\sqrt{x_0}}|\leqslant\dfrac{1}{\sqrt{x_0}}|x-x_0|.$$ 要使 $|f(x)-A|<\epsilon$，只要 $|x-x_0|<\sqrt{x_0}\epsilon$ 且 $x\geqslant0$，而 $x\geqslant0$ 可用 $|x-x_0|\leqslant x_0$ 保证，因此取 $\delta=\min\{x_0,\sqrt{x_0}\epsilon\}$（这个式子表示，$\delta$ 是 $x_0$ 和 $\sqrt{x_0}\epsilon$ 两个数中较小的那个数），则当 $x$ 适合不等式 $0<|x-x_0|<\delta$ 时，对应的函数值 $\sqrt{x}$ 就满足不等式 $$|\sqrt{x}-\sqrt{x_0}|<\epsilon$$ 所以 $$\lim\limits_{x\to x_0}\sqrt{x}=\sqrt{x_0}.$$ $\quad$ 上述 $x\to x_0$ 时函数 $f(x)$ 的极限概念中，$x$ 是既从 $x_0$ 的左侧也从 $x_0$ 的右侧趋于 $x_0$ 的。但有时只能或只需考虑 $x$ 仅从 $x_0$ 的左侧趋于 $x_0$（记作 $x\to x^- _0$）的情形，或 $x$ 仅从 $x_0$ 右侧趋于 $x_0$ （记作 $x\to x^+_0$）的情形。在 $x\to x^-_0$ 的情形，$x$ 在 $x_0$ 的左侧，$x<x_0$。$ \lim\limits_{x\to x_0}f(x)=A$ 的定义中，把 $0<|x-x_0|<\delta$ 改为 $x_0-\delta<x<x_0$，那么 $A$ 就叫做函数 $f(x)$ 当 $x\to x_0$ 时的**左极限**，记作 $ \lim\limits_{x\to x^-_0}f(x)=A$ 或 $f(x^-_0)=A$。 $\quad$ 类似的，在 $ \lim\limits_{x\to x_0}f(x)=A$ 的定义中，把 $0<|x-x_0|<\delta$ 改为 $x_0<x<x_0+\delta$，那么 $A$ 就叫做函数 $f(x)$ 当 $x\to x_0$ 时的**右极限**，记作 $ \lim\limits_{x\to x^+_0}f(x)=A$ 或 $f(x^+_0)=A$。 $\quad$ 左极限和右极限统称为**单侧极限**。 $\quad$ 根据 $x\to x_0$ 时函数 $f(x)$ 的极限的定义以及左极限和右极限的定义，容易证明：函数 $f(x)$ 当 $x\to x_0$ 时极限存在的充要条件是左极限及右极限各自存在并且相等，即 $$f(x^-_0)=f(x^+_0).$$ 因此，即使 $f(x^-_0)$ 和 $f(x^+_0)$ 都存在，但若不相等，则 $ \lim\limits_{x\to x_0}f(x)$ 也不存在。 例6. 设 $$y=f(x)=\begin{cases}x-1&x<0,\\0&x=0,\\x+1 &x>0.\end{cases}$$ 证明：当 $x\to 0$ 时，$f(x)$ 的极限不存在。 证 $\quad$ 仿例 $3$ 可证当 $x\to 0$ 时 $f(x)$ 的左极限 $$\lim\limits_{x\to 0^-}f(x)=\lim\limits_{x\to 0^-}(x-1)=-1,$$ 而右极限 $$\lim\limits_{x\to 0^+}=\lim\limits_{x\to 0^+}(x+1)=1,$$ 因为右极限和左极限存在但不相等，所以 $\lim\limits_{x\to 0}f(x)$ 不存在，如下图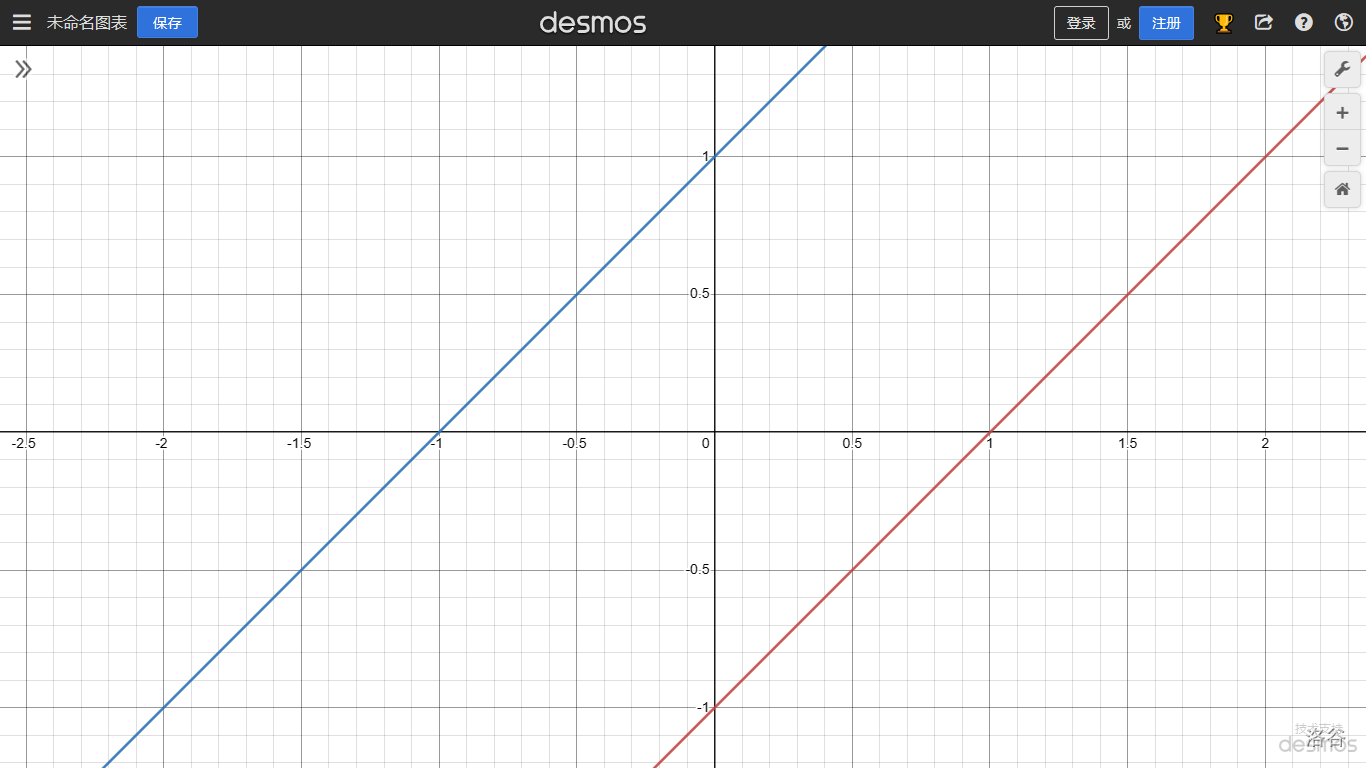：![](https://cdn.luogu.com.cn/upload/image_hosting/bwpqnhny.png) ## 自变量趋于无穷大时函数的极限 $\quad$ 如果在 $x\to\infty$ 的过程中，对应的函数值 $f(x)$ 无限接近于确定的数值 $A$，那么 $A$ 叫做函数 $f(x)$ 当 $x\to\infty$ 时的极限。精确地说，就是 **定义 $2\quad$ 设函数 $f(x)$ 当 $|x|$ 大于某一正数时有定义。如果存在常数 $A$，对于任意给定的正数 $\epsilon$（无论它多么小），总存在正数 $X$，使得当 $x$ 满足不等式 $|x|>X$ 时，对应的函数值 $f(x)$ 都满足不等式** $$|f(x)-A|<\epsilon$$ ### 那么常数 $A$ 就叫做函数 $f(x)$ 当 $x\to\infty$ 时的极限，记作 $$\lim\limits_{x\to\infty}f(x)=A\quad or\quad f(x)\to A(x\to\infty).$$ $\quad$ 定义 $2$ 可简单表达为 $\lim\limits_{x\to\infty}f(x)=A\Leftrightarrow\forall\epsilon>0,\exists X>0$，当 $|x|>X$ 时，有 $|f(x)-A|<\epsilon$。 $\quad$ 如果 $x>0$ 且无限增大（记作 $x\to+\infty$），那么只要把上面定义中的 $|x|>X$ 改为 $x>X$，就可得 $\lim\limits_{x\to+\infty}f(x)=A$ 的定义。同样，如果 $x<0$且 $|x|$ 无限增大（记作 $x\to-\infty$），那么只要把 $|x|>X$ 改为 $x<-X$ ，便得 $\lim\limits_{x\to-\infty}f(x)=A$ 的定义。 $\quad$ 从万恶的几何上来说，$\lim\limits_{x\to\infty}f(x)=A$ 的意义是：作直线 $y=A-\epsilon$ 和 $y=A+\epsilon$，则总有一个正数 $X$存在，使得当 $x<-X$ 或 $x>X$ 时，函数 $y=f(x)$ 的图形位于这两直线之间（由于作者手残，不会画图形，大概类似于一条心跳线）。这时，直线 $y=A$ 是函数 $y=f(x)$ 的图形的**水平渐近线**。 例7. 证明 $\lim\limits_{x\to\infty}\dfrac{1}{x}=0$。 证 $\quad\forall\epsilon>0$ ，要证 $\exists X>0$，当 $|x|>X$ 时，不等式 $$|\dfrac{1}{x}-0|<\epsilon$$ 成立。因这个不等式相当于 $$\dfrac{1}{|x|}<\epsilon\quad or\quad |x|>\dfrac{1}{\epsilon}.$$ 由此可知，如果取 $x=\dfrac{1}{\epsilon}$，那么当 $|x|>X=\dfrac{1}{\epsilon}$ 时，不等式 $|\dfrac{1}{x}-0|<\epsilon$ 成立，这就证明了 $$\lim\limits_{x\to\infty}\dfrac{1}{x}=0$$ $\quad$ 直线 $y=0$ 是函数 $y=\dfrac{1}{x}$ 的图形的水平渐近线。 # 函数极限的性质 $\quad$ 与收敛数列的性质相比较，可得函数极限的一些相应的性质。它们都可以根据函数极限的定义，运用类似于证明收敛数列性质的方法加一证明。由于函数极限的定义按自变量的变化过程不同有各种形式，下面以“$\lim\limits_{x\to x_0}f(x)$”这种形式为代表给出关于函数极限性质的一些定理，并就其中的几个给出证明。至于其他形式的极限的性质及其证明，只要相应的做一些修改即可得出 **定理 $1$（函数极限的唯一性）$\quad$ 如果 $\lim\limits_{x\to x_0}f(x)$ 存在，那么这极限唯一。** **定理 $2$（函数极限的局部有界性）$\quad$ 如果 $\lim\limits_{x\to x_0}f(x)=A$，那么存在常数 $M>0$ 和 $\delta>0$，使得当 $0<|x-x_0|<\delta$ 时，有 $|f(x)|<M$。** 证 $\quad$ 因为 $\lim\limits_{x\to x_0}f(x)=A$，所以取 $\epsilon=1$，则 $\exists\delta>0$，当 $0<|x-x_0|<\delta$ 时，有 $$|f(x)-A|<1 \Rightarrow |f(x)|\leqslant|f(x)-A|+|A|<|A|+1,$$ 记 $M=|A|+1$，则定理 $2$ 就获得证明。 **定理 $3$（函数极限的局部保号性）$\quad$ 如果 $\lim\limits_{x\to x_0}f(x)=A$，且 $A>0$（或 $A<0$），那么存在常数 $\delta>0$，使得当 $0<|x-x_0|<\delta$ 时，有 $f(x)>0$ （或 $f(x)<0$）。** 证 $\quad$ 就 $A>0$ 的情形证明。 $\lim\limits_{x\to x_0}f(x)=A>0$，所以，取 $\epsilon=\dfrac{A}{2}>0$，则 $\exists\delta>0$，当 $0<|x-x_0|<\delta$ 时，有 $$|f(x)-A|<\dfrac{A}{2}\Rightarrow f(x)>A-\dfrac{A}{2}=\dfrac{A}{2}>0.$$ 类似的，可以证明 $A<0$ 的情形。 从定理 $3$ 的证明中可知，在定理 $3$ 的条件下，可得下面更牛逼的结论 **定理 $3\;pro\quad$ 如果 $\lim\limits_{x\to x_0}f(x)=A(A\ne 0)$，那么就存在着 $x_0$ 的某一去心邻域 $\dot{U}(x_0)$，当 $x\in \dot{U}(x_0)$ 时，就有 $|f(x)|>\dfrac{|A|}{2}$。** 由定理 $3$，易得以下推论： **推论 $\quad$ 如果在 $x_0$ 的某去心邻域内 $f(x)\leqslant0$（或 $f(x)\geqslant0$），而且 $\lim\limits_{x\to x_0}f(x)=A

,那么 A\geqslant0（或 A\leqslant0）。**

证 \quad 设 \lim\limits_{x\to x_0}f(x)=A，则 \forall\epsilon>0,\exists\delta>0，当 0<|x-x_0|<\delta 时，有 |f(x)-A|<\epsilon。

$\quad$ 由假设， $x_n\ne x_0(n\in N_+)$，故当 $n>N$ 时，$0<|x_n-x_0|<\delta$，从而 $|f(x_n)-A|<\epsilon$。即 $\lim\limits_{n\to\infty}f(x_n)=A$。 本文结！ 后语：本文参考《高等数学》同济八版第一章第三节。 感兴趣的同学可以看一下[这里](https://zhuanlan.zhihu.com/p/258963587)