三角形的三心共线问题
EnofTaiPeople
·
·
学习·文化课
三角形的三心共线问题
第一部分:问题引入
重心 P:三角形三条中线的交点;
垂心 Q:三角形三条中线的交点;
外心 R:三角形三边的垂直平分线的交点。
本论文研究的是如上三角形三心的共线问题。
首先,在直角三角形中,垂心即直角上的顶点,外心即斜边上的中点,有定义可知,重心在两点所组成的中线上,于是三点共线,如图一。
我们猜想,在任意三角形中都有重心,垂心,外心,三点共线。
第二部分:前置知识及引理
知识一:相似三角形
定义:三角分别相等,三边成比例的两个三角形叫做相似三角形。
定理一:相似三角形任意对应线段的比等于相似比。
定理二:两边成比例且夹角相等的两个三角形相似。
定理三:三条边对应平行的两个三角形相似。
如图二,在 \triangle ABC 中,D 为 AC 中点,E 为 AB 中点。
于是,在 \triangle ABC 与 \triangle AED 中,
$\therefore\triangle ABC\sim\triangle AED$,且相似比为 $\frac{1}{2}$。
知识二:中位线
定义:连接三角形两边中点的线段。
如图二,$DE$ 便是 $\triangle ABC$ 的中位线,$\because\triangle ABC\sim\triangle AED\therefore\angle ADE=\angle ABC\therefore DE//BC$,
定理四:三角形中位线平行于对应边,长度是对应边的一半。
引理一:三角形中线上,顶点到重心的长度是重心到对边长度的两倍。
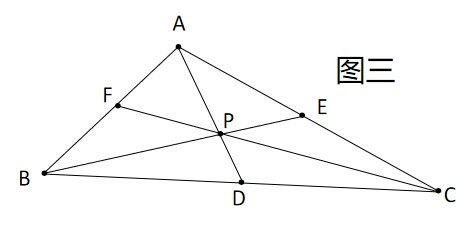
如图三,$P$ 为三角形重心,$\because BD=DC\therefore S_{\triangle BPD}=S_{\triangle CPD},S_{\triangle APB}=S_{\triangle APC}$,同理,$S{\triangle APB}=S_{\triangle APB}=S_{\triangle BPC}$,故 $S_{\triangle APB}=\frac{S_{\triangle ABC}}{3}$,$\therefore DP=\frac{AD}{3},AP=2DP$,引理成立。
引理二:三角形垂心到某顶点距离是外心到该顶点对边中点距离的两倍。
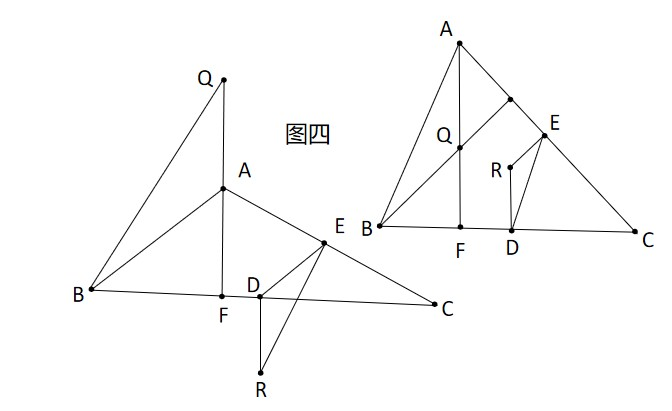
如图四,$DE$ 是 $\triangle ABC$ 的中位线,故 $DE//AB$,又$\because BQ\perp AC,ER\perp AC\therefore ER//BQ$,同理,$AQ//DR$,由定理三,$\triangle ABQ\sim\triangle DER$,又 $\because AB=2DE,\therefore AQ=2DR$,引理成立。
第三部分:解决问题
很明显,文章第二部分大多是针对非直角三角形的,而直角三角形的情况在开头就说明了。
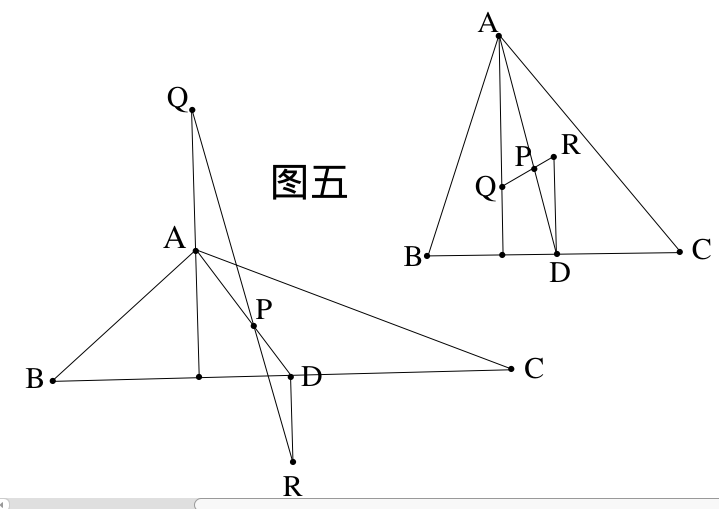
如图五,$\because AQ//DR,\therefore\angle PAQ=\angle PDR$,由引理一和引理二,$\frac{AP}{DP}=\frac{AQ}{DR}=2$,故 $\triangle PAQ\sim\triangle PDR,\angle APQ=\angle DPR$,又 $\because \angle QPD+\angle APQ=180\degree,\therefore \angle QPD+\angle DPR=180\degree,\therefore Q,P,R$ 三点共线。