Splay学习笔记
djwj233
2021-08-05 19:17:57
### Splay 的用途
Splay 是一种平衡树,因此:
- 同普通平衡树一样,它也能完成[P3369【模板】普通平衡树](https://www.luogu.com.cn/problem/P3369)中的所有功能;
- 不同的是,它还能支持对一个序列的区间进行一些奇妙的操作,比如[P3391 【模板】文艺平衡树](https://www.luogu.com.cn/problem/P3391)和[P3987 我永远喜欢珂朵莉~](https://www.luogu.com.cn/problem/P3987)等
- 不幸的是,它不能像 fhq-Treap 那样可持久化。
### Splay 的原理
Splay 是一种**通过旋转维护平衡**的平衡树。
不同于 Treap 等树的是,Splay 每次操作都要**把需要操作的结点旋转到根上**,这使它的旋转异常复杂。

~~再丢出这张窝自制的图~~
这是 Treap 进行旋转的方法,被称为**单旋**。
这里借一张[Menci 博客](https://oi.men.ci/splay-notes-1/)里的图,表示 Splay 中的单旋。

单旋 $\texttt{rotate(x)}$ 的过程:(这里以右旋为例)
- 将**自己**连到**祖父**($\texttt{a[a[x].fa].fa}$)上;
- 将自己的**右儿子**连到原先的**父亲**上(也就是替代了自己);
- 将**父亲**连到**自己**上(也就是替代了右儿子)
```c++
void Splay::rotate(int x) {
int f=a[x].fa, c=which(x);
a[a[f].fa].ch[which(f)]=x, a[x].fa=a[f].fa;
a[f].ch[c]=a[x].ch[c^1], a[a[x].ch[c^1]].fa=f;
a[x].ch[c^1]=f, a[f].fa=x;
update(f), update(x); //注意一定要先更新f再更新x
}
```
但是,如果维护 Splay 只采用单旋是不对的,考虑原树是一条单链的情况,如果我们每次访问链最底部的一个点把它转到根,那么时间复杂度将会达到 $\Theta(n^2)$。
(实际上,单旋 Splay 被称为 Spaly,是假算法,在[HNOI2017](https://www.luogu.com.cn/problem/P3721)中出现过)
那么,Splay 的**双旋**应运而生。简单地说,双旋就是**先单旋一次父亲、再单旋一次自己**。
如果我们的目标是把 $x$ 转上去,那么双旋的处理分为以下的六种情况:(图源 OI-wiki)

- 1/2 两种只需一次单旋 $\texttt{rotate(x)}$ 即可完成。
- 3/4 两种需要两次**相同方向、不同节点**的单旋 $\texttt{rotate(y)}$,$\texttt{rotate(x)}$ $\texttt{}$,被称为**一字型旋转**;
- 5/6 两种需要两次**不同方向、相同节if(a[f].fa) if(a[f].fa) if(a[f].fa) 点**的单旋 $\texttt{rotate(x)}$,$\texttt{rotate(x)}$,被称为**之字型旋转**。
现在引入 $\texttt{splay(x)}$ 操作为**通过一系列双旋将 $x$ 移到 $root$ 处**。(此操作在中文中被称为**伸展**,这也是 Splay 中文名**伸展树**的由来)
```c++
void Splay::splay(int x) {
for( int f=a[x].fa ; f ; f=a[x].fa ) {
if(a[f].fa) rotate( which(x)==which(f) ? f : x );
rotate(x);
} rt=x;
}
```
最后一定要注意**每次操作后必须 $\texttt{splay}$ !!!**
(时间复杂度分析放在基本操作之后)
### Splay 的基本操作
这里依旧以[P3369 【模板】普通平衡树](https://www.luogu.com.cn/problem/P3369)为例。
- 单个结点
我们采取`ch[0/1]`的方式分别代表结点的左儿子、右儿子,并记录了每个结点的父亲。
```c++
struct node {
int fa,ch[2];
int val;
int siz,cnt;
} a[N]; int tot,rt;
```
- 更新结点信息与基本操作
$\texttt{which}$ 操作询问了 $x$ 是其父亲的左结点还是右结点,这可以大大减少代码量。
```c++
int Splay::New(int v) {
a[++tot].val=v, a[tot].siz=a[tot].cnt=1;
return tot;
}
void Splay::update(int x) {
a[x].siz=a[a[x].ch[0]].siz+a[a[x].ch[1]].siz+a[x].cnt;
}
int Splay::which(int x) { return a[a[x].fa].ch[1]==x; }
```
- 单旋与双旋**(重点)**
见上。
- 插入
**注意不能在第 12 行后 $\texttt{splay}$**,否则会变成递归地把每个结点旋到根。
然后因为 $\texttt{splay}$ 的过程中已经 $\texttt{update}$ 过所有结点了,因此最后不用再 $\texttt{update}$。
```c++
void Splay::insert(int &x,int f,int v)
{
if(x==0) {
x=New(v), a[x].fa=f;
splay(x); return ;
}
if(v<a[x].val) insert(a[x].ch[0],x,v);
else if(v==a[x].val) {
a[x].cnt++, splay(x);
return ;
}
else insert(a[x].ch[1],x,v);
}
```
- 查值与查排名
```c++
int Splay::getRank(int x,int v)
{
if(x==0) return 1;
if(v<a[x].val) return getRank(a[x].ch[0],v);
else if(v==a[x].val) {
int res=a[a[x].ch[0]].siz+1;
splay(x); return res;
} else {
int res=a[a[x].ch[0]].siz+a[x].cnt;
return res+getRank(a[x].ch[1],v);
}
}
int Splay::getVal(int x,int v)
{
if(x==0) {
splay(x); return a[x].val;
}
if(v<=a[a[x].ch[0]].siz) return getVal(a[x].ch[0],v);
else if(v<=a[a[x].ch[0]].siz+a[x].cnt) {
splay(x); return a[x].val;
} else return getVal(a[x].ch[1],v-a[a[x].ch[0]].siz-a[x].cnt);
}
```
- 查前驱、后继
以前驱为例,我们可以通过**新插入一个结点,查前驱,再删除**的方式。
对已经在树中的结点查前驱十分方便,只需 $\texttt{splay}$ 后在左子树中向右走到底即可。
```c++
int Splay::getPre() {
int p=a[T.rt].ch[0];
while(a[p].ch[1]) p=a[p].ch[1];
splay(p); return p;
}
int Splay::getNxt() {
int p=a[T.rt].ch[1];
while(a[p].ch[0]) p=a[p].ch[0];
splay(p); return p;
}
```
主函数中:
```c++
T.insert(T.rt,0,x);
printf("%d\n",T.a[T.getPre()].val);
T.erase(x);
```
- 删除**(重点)**
我们先把要删除的结点 $\texttt{splay}$ 到根(这可以用一次 $\texttt{getRank}$ 实现),然后:
1. 如果其 $cnt$ 值不小于 $2$,直接减去 $1$,然后 $\texttt{update}$;
2. 否则,如果它没有左儿子或没有右儿子,则直接用另一个儿子替换它;
3. 否则,将其左右儿子的两棵子树**合并**。
那么怎么合并呢?我们**把左子树中最大的数 $\texttt{splay}$ 上来当作新的根**,那么原来的根一定在新根的右儿子处,直接将它删去即可。
```c++
void Splay::erase(int v){ getRank(T.rt,v); if(a[T.rt].cnt>1) { a[T.rt].cnt--, update(T.rt); return ; } if(a[T.rt].ch[0]==0) { T.rt=a[T.rt].ch[1], a[T.rt].fa=0; return ; } if(a[T.rt].ch[1]==0) { T.rt=a[T.rt].ch[0], a[T.rt].fa=0; return ; } int cur=T.rt, x=getPre(); a[a[cur].ch[1]].fa=T. rt; a[x].ch[1]=a[cur].ch[1]; update(x);}
```
### Splay 的时间复杂度
事实上,我们可以证明:**Splay 单次操作的时间复杂度是 $\mathcal O(\log n)$ 的**。
##### 一些定义与约定
由于每次操作后都要把结点 $\texttt{splay}$ 到根,因此**在操作中访问的结点都会在 $\texttt{splay}$ 中被再次访问**。因此,操作的复杂度和旋转的复杂度相同。
我们记 $|x|$ 为以 $x$ 为根的子树的大小(为区分,后文有时用 $siz(x)$ 代替),并记 $n=|root|$。
记 $\Phi$ 为整棵 Splay(记为 $T$)的势能函数,$\phi(x)$ 为单个结点的所具有的势能。定义:
$$
\phi(x)=\log |x|,\ \Phi=\sum\limits_{i=1}^n \phi(x)
$$
可以发现,对任意点 $x$ 有 $|x|\le n$,因此 $\Phi\le \sum_{i=1}^n \log n=n\log n$。
另外,我们在这里认为:**单次 $\texttt{rotate}$ 的时间复杂度恒为 $\mathcal O(1)$**。
##### 单旋
由于 $\texttt{zag}$ 和 $\texttt{zig}$ 相类似,我们这里只分析 $\texttt{zig}$ 的复杂度。
我们设当前要进行操作的点为 $x$,其父亲为 $y$。如下图:(图是自己做的,巨丑)

我们令旋转之后二者的势能分别为 $\phi^\prime(x),\phi^\prime(y)$,那么我们有:
$$
\Delta\Phi=\phi^\prime(x)+\phi^\prime(y)-\phi(x)-\phi(y)
$$
由于转完后,$\textrm{subtree}^\prime(x)$ 包含了原先 $\textrm{subtree}(y)$ 中所有的结点,因此有 $\phi^\prime(x)=\phi(y)$;
又因为转完后 $y$ 是 $x$ 的子节点,因此 $siz^\prime(y)\le siz^\prime(x)$,可知 $\phi^\prime(y)\le \phi^\prime(x)$;
代入上式可得:
$$
\Delta\Phi\le\mathcal O(1)+\phi^\prime(x)-\phi(x)
$$
##### 一字型旋转
同上,由于 $\texttt{zag-zag}$ 和 $\texttt{zig-zig}$ 相类似,我们这里只分析 $\texttt{zig-zig}$ 的复杂度。
同样,我们设当前要进行操作的点为 $x$,其父亲为 $y$,祖父为 $z$。
由于一字型旋转涉及两次 $\texttt{rotate}$,因此有:
$$
\Delta\Phi=\mathcal O(1)+\phi^\prime(x)+\phi^\prime(y)+\phi^\prime(z)-\phi(x)-\phi(y)-\phi(z)
$$
模拟旋转过程有:
- $\phi^\prime(x)=\phi(z)$;
- $\phi^\prime(z)\le\phi^\prime(y)\le\phi^\prime(x)$;
- $\phi(z)\ge\phi(y)\ge\phi(x)$。
代入:
$$
\Delta\Phi\le \mathcal O(1)+2(\phi^\prime(x)-\phi(x))
$$
但是,这个上界是不精准的,因为我们在下面求和时如果把这个 $\mathcal O(1)$ 带进去会炸掉。怎么办呢?
我们退回一步,并忽略 $2$ 这个常系数:
$$
\Delta \Phi\le \mathcal O(1)+\phi^\prime(x)+\phi^\prime(z)-2\phi(x)
$$
- **引理:$\phi(x)+\phi^\prime(z)-2\phi^\prime(x)<-1$**
> 证明:即证 $\log siz(x)+\log siz^\prime(z)-2\log siz^\prime(x)<-1$,也即 $\log \dfrac{siz(x)siz^\prime(z)}{siz^\prime(x)^2}<-1$。
>
> 画出旋转的图示,我们发现**旋转前后 $\operatorname{subtree}_x$ 和 $\operatorname{subtree}^\prime_z$ 不相交且不包含点 $y$**,即 $siz(x)+siz^\prime(z)<siz^\prime(x)$。
>
> 由 $\log$ 的单调性,$\log \dfrac{siz(x) siz^\prime(z)}{siz^\prime(x)^2}<\log \dfrac{siz(x)siz^\prime(z)}{(siz(x)+siz^\prime(z))^2}\le\log \dfrac{1}{2}\le-1$。证毕。
两式相加可得:
$$
\Delta\Phi\le \mathcal O(1)-1+\phi^\prime(x)-\phi(x)
$$
因为势能函数中的常数是可以设的,所以我们也可以设 $\phi(x)=C\log siz(x)$,这样 $1$ 可以变成任意的常数,将 $O(1)$ 约去。
总之我们有:
$$
\Delta\Phi\le \phi^\prime(x)-\phi(x)
$$
##### 之字形旋转
这里只分析 $\texttt{zig-zag}$,并设当前要进行操作的点为 $x$,其父亲为 $y$,祖父为 $z$。
同上有:
$$
\Delta\Phi=\mathcal O(1)+\phi^\prime(x)+\phi^\prime(y)+\phi^\prime(z)-\phi(x)-\phi(y)-\phi(z)
$$
$$
\Delta \Phi\le \mathcal O(1)+\phi^\prime(x)+\phi^\prime(z)-2\phi(x)
$$
**但是,在引理 $\phi(x)+\phi^\prime(z)-2\phi^\prime(x)<-1$ 的证明中,$siz(x)+siz^\prime(z)<siz^\prime(x)$ 性质并不成立,我们需要找一个性质别的换掉**。
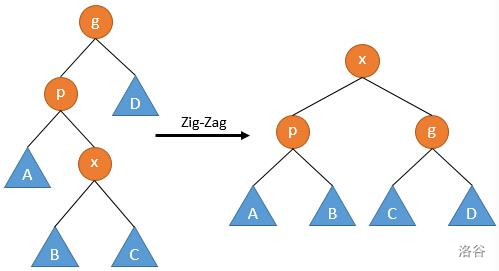
(图源[这篇博客](https://www.luogu.com.cn/blog/Atalod/shi-jian-fu-za-du-shi-neng-fen-xi-qian-tan),其中 $p,g$ 分别等价于本文中的 $y,z$)
观察可知,可以把它换为 $siz^\prime(x)>siz^\prime(y)+siz^\prime(z)$,那么可得:
$$
\phi^\prime(y)+\phi^\prime(z)-2\phi^\prime(x)<-1
$$
因此,我们不应该像上面那样代入,应换成:
$$
\Delta \Phi\le \mathcal O(1)+\phi^\prime(y)+\phi^\prime(z)-2\phi(x)
$$
这样就能推出:
$$
\Delta\Phi\le \phi^\prime(x)-\phi(x)
$$
##### 总结
通过以上的证明,我们得到:对所有的点 $x$ 进行 $\texttt{rotate}$ 操作,其消耗的势能不大于 $\phi^\prime(x)-\phi(x)$。
因此,设一次 $\texttt{splay}$ 中涉及的点从浅到深为 $x_{1\cdots m}$,那么它的总复杂度为:
$$
\mathcal O(1)+\sum\limits_{i=2}^m (\phi^\prime(x_i)-\phi(x_i))
$$
其中,前面的 $\mathcal O(1)$ 是因为单旋仅在 $fa_x$ 为根时出现,最多一次。而单旋 Splay 的复杂度中前面一项是 $\Theta(m)$,这也是它假掉的原因。
由于 $\texttt{splay}$ 中 $\texttt{rotate}$ 后 $x$ 会代替 $fa_x$,换言之有 $siz^\prime(x_i)=siz(x_{i-1})$。那么总复杂度等于:
$$
\mathcal O(1)+\sum\limits_{i=2}^m (\phi(x_{i-1})-\phi(x_i))
$$
消掉其中大多数项,答案变为:
$$
\mathcal O(1)+\phi(x_1)-\phi(x_m)\le \mathcal O(1)+\phi(x_1)
$$
由于 $|x_1|=|root|=n$,因此总复杂度为 $\mathcal O(\log n)$。
- 以上内容部分参考了[这个问题](https://www.zhihu.com/question/40777845)中的回答和[Mr.Spade的博客](https://www.cnblogs.com/Mr-Spade/p/9715203.html)
### Splay 的应用
如果将 Splay 作为一棵普通平衡树,它不仅常数大还难调,并不优秀。
实际上,与其它普通平衡树不同,Splay **允许自由旋转的特性**使它可以支持一些区间上的操作。
##### 区间翻转
这是 Splay 的标志性应用,一般来讲,带有**区间翻转**字样的题目都可以考虑 Splay。
- [P3391 【模板】文艺平衡树](https://www.luogu.com.cn/problem/P3391)
这里是用 Splay 维护**区间翻转问题**的模板。
我们建一个 Splay,里面存的是**位置**,即 $[1,n]$ 中的每个坐标。
每次我们要对区间 $[l,r]$ 进行翻转操作时,我们**先将 $l-1$ 旋到根,再将 $r+1$ 旋到根的右结点**。这样树就变成了这样:

这样,当前**根结点右儿子的左子树**就是我们要操作的区间。
那么我们借用线段树 Lazy-Tag 的思想,当执行将一棵子树翻转时,**给它打上一个 *tag*,然后访问到时像线段树那样下传**。
这里必须注意:**不能用 *val* 的值来判断,需要用 *siz* 的值决定递归到哪个子树中**。
因此,我们实际询问的点是:$l,\ r+2$。这里由于我们要实现**将一个点旋到根的右结点**的功能,我们需要将 $\texttt{splay}$ 魔改一下:
```c++
void splay(int p,int t) { // t=0 or t=rt
for( int f=a[p].fa ; f!=t ; f=a[p].fa ) {
if(a[f].fa!=t) rotate( which(f)==which(p) ? f : p );
rotate(p);
}
if(a[p].fa==0) rt=p;
}
```
此外,由于翻转区间两次相当于没有进行操作,我们可以采用异或的方式维护 *tag*。
最后,我们中序遍历一遍 Splay 即可。
[Code](https://www.luogu.com.cn/record/55592104)
##### Lazy-Tag 的综合使用
- [P2042 [NOI2005] 维护数列](https://www.luogu.com.cn/problem/P2042)
怎么早年的 NOI 全是这些莫名奇妙的题
先咕着。
##### Splay in Ynoi
- [P3987 我永远喜欢珂朵莉~](https://www.luogu.com.cn/problem/P3987)
如果把修改中要求的 $x$ 的倍数去掉,那就是一个经典问题。
但这里要求是 $x$ 的倍数,因此考虑继续沿用**只除不乘**的性质。注意到总的除法次数至多是 $\mathcal O(n\log a_i)$,于是考虑维护。
对每个整数 $x$,将它的倍数的下标都扔进一棵 Splay 里,每次要除时直接把对应的 Splay 中区间 $[l,r]$ 截出来暴力处理即可。
这样可以做到 $\mathcal O(n\log a_i\log n)$,但是这样常数极大且实现复杂。
可以用 `vector` + 并查集换掉 Splay 来优化代码。
[Code](https://www.luogu.com.cn/record/58610153)